International Journal of Cancer and Clinical Research
Estimating Relapse Free Survival as a Net Probability: Regression Models and Graphical Representation. An Application of a Large Breast Cancer Case Series
Annalisa Orenti1, Elia Biganzoli1,2* and Patrizia Boracchi1
1Department of Clinical Sciences and Community Health, University of Milan, Italy
2Unit of Medical Statistics, Biometry and Bioinformatics, National Cancer Institute of Milan, Milan, Italy
*Corresponding author:
Elia Biganzoli, Laboratory of Medical Statistics, Epidemiology and Biometry G. A. Maccacaro, Department of Clinical Sciences and Community Health, University of Milan, Italy; Unit of Medical Statistics, Biometry and Bioinformatics, National Cancer Institute of Milan, Milan, Italy, Campus Cascina Rosa, Via Vanzetti 5, 20133, Milano, Italia, E-mail: elia.biganzoli@unimi.it
Int J Cancer Clin Res, IJCCR-3-063, (Volume 3, Issue 4), Original Article; ISSN: 2378-3419
Received: January 30, 2016 | Accepted: August 10, 2016 | Published: August 12, 2016
Citation: Orenti A, Biganzoli E, Boracchi P (2016) Estimating Relapse Free Survival as a Net Probability: Regression Models and Graphical Representation. An Application of a Large Breast Cancer Case Series. Int J Cancer Clin Res 3:063. 10.23937/2378-3419/3/4/1063
Copyright: © 2016 Orenti A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In most clinical studies, the evaluation of the effect of a therapy and the impact of prognostic factors is based on relapse-free survival. Relapse free is a net survival, since it is interpreted as the relapse-free probability that would be observed if all patients experienced relapse sooner or later. Death without evidence of relapse prevents the subsequent observation of relapse, acting in a semi-competing risks framework. Relapse free survival is often estimated by standard regression models after censoring times to death. The association between relapse and death is thus accounted for. However, to better estimate relapse free survival, a bivariate distribution of times to events needs to be considered, for example by means of copula models. We concentrate here on the copula graphic estimator, for which a pertinent regression model has been developed. No direct parametric estimation of the regression coefficient for the covariates is available and the evaluation of the impact of covariates on relapse free survival is based on graphical representation for each covariate singularly. The advantage of this approach is based on the relationship between net survival, and crude cumulative incidences. Regression models can be fitted for the latter quantities and the estimates can be used to compute net survival through a copula structure. Our proposal is based on flexible regression transformation model on crude cumulative incidences based on pseudo-values. An overall view of the joint association among covariates and relapse free survival is obtained through Multiple Correspondence Analysis. Moreover cluster analysis on MCA coordinates was used to synthesize covariate patterns and to estimates the corresponding relapse free survival curve. This approach has been applied to a large "historical" case series of patients with breast cancer.
Keywords
Relapse free survival, Semi-competing risks, Copula, Multivariate analysis, Breast cancer
Introduction
In most clinical studies, the evaluation of the effect of a therapy or the impact of prognostic factors is based on the time elapsed form the date of disease diagnosis or the beginning of treatment and the occurrence of different events related to the disease progression.
A first analysis on event free survival is often based on the comprehensive end-point in which all possible events are considered. Then subsample of events are also considered as end-points aiming to a deeper investigation of the treatment effect. An example in cancer studies is relapse free survival where the interest is the estimation of the probability to be free of tumour recurrence during follow-up. Looking to breast cancer, tumour recurrence is a composite end-point in which the occurrence of local relapses, contralateral tumours and distant or local metastases are frequently considered. The occurrence of death not related to the disease or secondary tumours different from breast cancer (defined as absorbing events) may be observed for some patients before tumour relapse and prevent the observation of the main end-point. On the contrary the occurrence of relapses does not prevent the observation of absorbing events. This situation is usually referred to as "semi-competing risks" [1]. In the absence of independent censoring, times to absorbing events are always observable and the incomplete observation relies only to relapse.
Relapse free survival is commonly estimated by Kaplan-Meier method considering time to occurrence events which are not included into the end-point as censored. It is an estimate of the marginal (net) survival function, i.e. the survival free from relapses in an hypothetical situation where the events of interest can be observed for all patients. In such a context, the use of Kaplan-Meier method is correct only in the case of independence among times to tumour recurrences and times to competing events, otherwise the knowledge of the multivariate distribution of time to events is needed.
It can be assumed that if no absorbing events occurred before relapse, time to relapse and the time to absorbing events would be observed for all patients giving the complete "bivariate" distribution whose relevant characteristic is the structure of the association between time to relapse and time to absorbing events.
As in semi-competing risks settings time to relapse can be only partially observable, a proposed solution is based on the assumption of a particular structure of the bivariate distribution. To avoid too rigid assumptions flexible structures may be preferred and this is the reason for which Copulas are arising a growing interest. Copulas are functions that join bivariate distribution functions to their univariate marginal uniform distribution functions [2,3], in this case the distribution of time to relapse and the distribution of time to absorbing events. An advantage of copulas is that the marginal distributions do not need to be defined, thus they can be parametric or non parametric as well. As Copulas are not directly estimable from semi-competing risks data, the proposed solution is to recur to their relationship with estimable functions i.e., crude cumulative incidences of relapse and absorbing events. Generally, crude cumulative incidence of a specific event is the probability of observing such an event as the first [4].
Several copula functions can be used to estimate net survival in clinical applications [2], but Archimedean Copulas are convenient because of the availability of a simple closed form estimator based on the relationship between copulas, overall survival and crude cumulative incidences [5]. A key parameter of copula functions is related to the association among times to different events. In the case of semi-competing risks setting some association estimators can be applied [1,6,7] and in the case of Clayton Copula a strong consistent estimator has been proposed [1].
In the presence of competing risks a regression model based on Copula graphical estimator has been proposed by Lo and Wilke [5]. The advantage of the proposal is the possibility to use regression models on cause specific hazards, sub distribution hazards, crude cumulative incidences (parametric or semi-parametric) and to combined results given a copula structure to evaluate the covariate effects on net survival.
Lo and Wilke showed the use of both parametric and semi-parametric modes based on crude cumulative incidences and referred the possibility of the indirect estimation of crude cumulative incidences through cause specific hazards. In their method the evaluation of covariates impact on net survival is not based on the estimation of regression coefficients but on a graphical representation of the estimated marginal survival as a function of each single covariate levels (fixing the remaining covariates to their mean values).
In our approach, we adopted regression models on crude cumulative incidences pseudo values [8] including regression splines for estimating the shape of baseline, avoiding rigid assumptions on the shape of crude cumulative incidence curves and allowing flexibility. A log link was used to obtain a simple interpretation of model results in terms of relative risks [9]. Concerning the graphical representation, we first adopted a multivariate technique (multiple correspondence analysis) to represent the joint relationship among covariates in a plane (factorial plane). Then we projected the estimated marginal relapse free probabilities on the factorial plane, having the advantage of visualizing the relationship among relapse free survival and the whole set of covariates. Moreover, to summarize the multivariate structure, cluster analysis is performed in such a way to represents the estimated net survival probability curves as a function of identified patient's profiles.
To show the procedure we used a large dataset of breast cancer with available long and accurate follow-up and information on main clinical and pathological characteristics.
Methods
Latent failure times and relationship among time functions
At the beginning of follow-up each patient is considered at risk for relapse and absorbing events, each one occurring to "latent" or "potential" failure times .
The joint "survival" function i.e. the probability of relapsing after time and having an absorbing event after is:
The survival probability at time t for relapse and absorbing events (overall survival) is:
It can be shown that the marginal distribution of YR from S(t) is a proper survival distribution in the hypothetical condition where the absorbing event before relapse has been removed:
This is the net survival function for relapse [4]. It is worth noting that in the case of independence the overall survival equals the product of net survivals for relapse and absorbing events.
The marginal distribution of is always observable and is expressed as
The crude cumulative incidence of relapse, i.e. the probability that relapse is observe as first event, is:
In analogy the crude cumulative incidence of absorbing events is
The relationship between overall survival and crude cumulative incidences of relapse and absorbing events is:
It is worth of note that overall survival and crude cumulative incidences are estimable also when and are only known.
Copulas
Concerning time to relapse and time to absorbing events, the general representation of Archimedean Clayton Copula [10] is:
Given an Archimedean copula, marginal survival can be estimated by crude cumulative incidences [11].
Considering the discrete time nature of the observed data, an empirical estimator can be written as follows:
where can be estimated by the method for competing risks [12] and can be estimated by Kaplan-Meier Method on "overall event", or by crude cumulative incidences as reported in (1).
In the presence of covariates the approach has been generalized by Lo and Wilke by modelling crude cumulative incidences in function of covariates and plugging the estimates in (2).
From a practical perspective, in the case of a covariate xp. measured on qualitative or ordinal scale it is possible to trace for different values of xp and in the case of a covariate measured on a continuous scale a "binning" approach could be used.
The association between non terminal and terminal event
With semi-competing risks data, the dependence between time to relapse and time to absorbing events provides information about the extent to which the occurrence of a relapse hastens the occurrence of absorbing events. Specific approaches for estimating this association have been proposed in the literature and have to be adopted in a semi-competing risks analysis, by specifying the form of the bivariate distribution of times to events [1,6,7].
Given a time to relapse and a time to absorbing events , the parameter θ can be interpreted as the ratio between the instantaneous risk of absorbing events at time , given absorbing events has not occurred till and relapse has occurred at time , and the instantaneous risk of absorbing events at time , given absorbing events has not occurred till and relapse has not occurred till . The ratio between the two above mentioned instantaneous risks is supposed to be constant in time. A positive value of θ indicates that the occurrence of relapse increases the risk of absorbing events. A null value of θ indicates that time to relapse and time to absorbing events are independent.
Modelling crude cumulative incidences by pseudo-values
Crude cumulative incidences can be modelled by transformation models:
Where g is the link function, is the "baseline" and is the linear predictor for covariates effect.
Models estimates can be obtained recurring to pseudo-values of crude cumulative incidences [8]. Firstly J time points are chosen from follow-up times: . Then, for the event k (k = 1,2) and for the time the pseudo value for each subject s (s = 1,...,n) is defined as follows:
where is the non parametric estimate of crude cumulative incidence at on the whole sample and is the corresponding estimate obtained after deleting the subject s from the sample. can be modelled by a vector y of J-1 dummy variables or, to obtain a smoothed shape, by regression splines [13]
For each subject J pseudo-values are calculated, thus for a sample of n subjects a matrix of rows is considered for the regression model. Taking into account the correlation among pseudo-values of the same subject, generalized estimating equations (GEE) can be used. Different structures for the correlation are available in standard software which can be considered, nevertheless no substantial influence of the structure on the final model estimates have been shown [8].
Different link functions allow to obtain clinically useful measures by a simple relationships with model regression coefficients (see [9] for details).
Because of the easily interpretation of relative risk, the log link was used for modelling crude cumulative incidences. For the implementation R software was used: package "pseudo" for obtaining pseudo-values for crude cumulative incidences, package "geepack" (function geese) for model estimation with the following options: family Gaussian, link log, scale. fix = TRUE, scale. value = 1, package "rms" (function rcspline. eval) for including splines bases into the model.
Evaluation of model fitting
As the marginal survival for relapse depends on the estimated crude cumulative incidences, model fitting evaluation for pseudo-values models were performed for both relapse and absorbing events. A graphical approach was applied to compare observed and expected crude cumulative incidences. Firstly for each one of fixed times used for calculating pseudo-values and for each subject s, the estimated crude cumulative incidence is obtained by gee model results on the basis of subject covariate vector . Then, for each time, the expected crude cumulative incidence is calculated as: The observed incidences are obtained by non parametric estimated crude cumulative incidences on the whole case series.
Visualization of the relationship among covariates and marginal survival
The approach proposed by Lo and Wilke allows to evaluate the relationship between marginal survival and each covariate by graphical representation of survival curves by fixing, as an example, the remaining covariates to their mean values.
This is useful for the effect of the single covariate but it does not allow to evaluate the covariate's joint effect. To this aim the estimated marginal survival probabilities can be represented on a graph which summarizes the data structure: in the case of both continuous and categorical covariates multiple correspondence analysis (MCA) plot.
MCA is an exploratory multivariate technique which allows to visualize the association structure of a multidimensional contingency table. Variables and subjects can be plotted onto a subspace (usually a plane) defined by the factorial axes, which mainly contribute to explain the total variability of the original data, according to new coordinates (factorial scores). Considering the origin of factorial axes, the angular distance among categories and subjects is related to their mutual associations. Subjects which are projected close together shared similar covariates pattern (row-profiles) and modalities of covariate which are projected close together shared similar joint preferences of subjects (columns-profiles) [14]. As MCA is based on categorical covariates then covariates measured on the continuous scales should be firstly categorised. To visualize the association between estimated marginal survival probabilities and the pattern of association among variables, estimates survival probabilities are plotted on the plane as passive variables, i.e they do not contribute to the identification of factorial axes but the position of their projected values on the plane allows to describe their association with the covariates association pattern [15]. As an aid to identify the characteristics of joint variable patterns which shared similar estimated marginal survival probabilities, values of these latter have been projected on the MCA plane by using a gray scale. This is a simplified version of the procedure reported in [16].
Presence of putative clusters of subjects can be identified by the visual inspection of the MCA plane but, for a more objective procedure, a cluster analysis can be performed on the subjects factorial scores (package FactoMineR). Finally to summarize the joint effect of covariates on estimated marginal survival, survival curves can be plotted for each identified cluster.
Results
Case series
Data regarding 654 women with small, non-metastatic primary breast cancer and submitted to surgery at the National Cancer Institute in Milan between 1985 and 1989 were analysed. All women received quadrantectomy, axillary dissection and radiotherapy (QUART), moreover axillary node positive women received adjuvant medical therapy: premenopausal and postmenopausal patients negative for estrogens receptors received chemotherapy, while postmenopausal patients positive for estrogens receptors received tamoxifen. All details of trials can be found in [17,18].
Endpoint of interest
Attention is focused here on time to relapse, such as intra breast tumour recurrence, omolateral or contralateral breast carcinoma and regional or distant metastases, because its distribution gives information on the progression of the disease and it is of concern in order to choice the best treatment strategy. The aim of the analysis is to evaluate the effect of covariates (axillary lymph nodes metastases, pathological tumour dimension, estrogens and progesterone receptor status and age) on relapse free survival.
In the case series the occurrence of primary tumours different from breast cancers during follow-up are considered as "absorbing events" because after their occurrence information on breast cancer relapse are no longer reported.
A related purpose is the evaluation of association between times to breast cancer relapse and times to "absorbing events". This quantity, although of potential clinical interest, is not evaluated in original articles.
Results
The association parameter between breast cancer relapse and absorbing events estimated by means of Fine's method is 7.18. This means that the association between the two events is quite high: people who experience a breast cancer relapse have an instantaneous risk of absorbing events about 7 times bigger than people who do not experience a relapse.
In order to estimate net relapse free survival by means of copula graphic estimator, crude cumulative incidences for relapse and for absorbing events have to be computed for each subject. 576 patients have complete information on the above mentioned clinical variables. For this purpose we fit a pseudo-values regression model on relapse crude cumulative incidence and a pseudo-values regression model on absorbing events crude cumulative incidence. For both events generalized estimation equations model with link log was used. Baseline for relapse crude cumulative incidence was modelled by a restricted cubic spline with 4 knots and baseline for absorbing events crude cumulative incidence was modelled by a restricted cubic spline with 3 knots. Knots positions were defined by quantiles of event times in the original dataset. The remaining covariates were included by dummy variables. Time dependent effects of covariates were investigated by including interaction terms between covariates and basis of spline functions for time baseline. No time dependent effects were found statistically significant, thus an additive model with fixed effects of covariates was considered. Model results were reported in tables 1 and table 2. It is worth of note that when modelling absorbing events the first two age class were joined as no events occurred in women less than 40 years, causing a non convergence of the model.
![]()
Table 1: Relapse crude cumulative incidence regression model based on pseudo-values. For each covariate the exponent of regression coefficient is estimate of the ratio between crude cumulative incidences. N0 and N1 indicates absence or presence of axillary lymph node metastases respectively. T is pathological tumour size (in cm). PgR +,- indicates > 25 or < = 25 femtomoles progesterone receptors per milligram of cytosolic protein respectively, ER +,- indicates > 10 fmoli or < = 10 of estrogen receptors femtomoles per milligram of cytosolic protein respectively and Time, time' and time'' represents spline basis for time.
View Table 1
![]()
Table 2: Absorbing events crude cumulative incidence regression model based on pseudo-values. For each covariate the exponent of regression coefficient is the estimate of the ratio between crude cumulative incidences. N0 and N1 indicates absence or presence of axillary lymph node metastases respectively. T is pathological tumour size (in cm). PgR +,- indicates > 25 or < = 25 femtomoles progesterone receptors per milligram of cytosolic protein respectively, ER +,- indicates >10 fmoli or < = 10 of estrogen receptors femtomoles per milligram of cytosolic protein respectively time and time' are the spline bases for time.
View Table 2
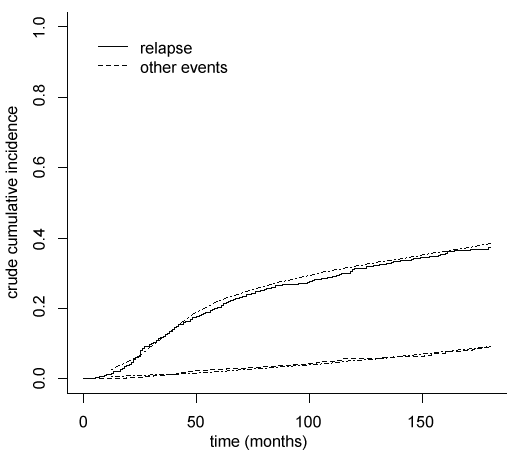
To evaluate the goodness of fit a calibration plot is drawn (Figure 1), where the mean of the crude cumulative incidences curves estimated for each subject by pseudo-values regression model are compared with the crude cumulative incidences obtained by non-parametric method of Kalbfleish and Prentice [12]. The results are very similar, proving that crude cumulative incidences are good estimated by the pseudo-values regression models.
The crude cumulative incidences estimated for each subject can be used to compute net relapse free survival, using a Clayton Archimedean copula, as given in formula (2).
To describe the association among clinical-pathological characteristics, a multiple correspondence analysis (MCA) is fitted. All covariates are used as active variables to obtain the plan of the first two factorial axes. Figure 2 summarize MCA results. The first factorial axis mainly contrasts women with positive and negative hormones receptors status. The second axis mainly contrasts women with no axillary lymph nodes metastases, small tumour and old age and women with axillary lymph nodes metastases, bigger tumour and young age. Women with negative estrogens receptors tend to have also negative progesterone receptors (upper right quadrant), women with age 50-60 years have frequently no axillary lymph nodes metastases and tumours less than 1 cm (lower right quadrant), youngest women tend to have biggest tumours with axillary lymph nodes metastases (upper quadrants), finally women aged between 41-50 or more than 60 tend to have positive hormones receptors and tumours of 1-2 cm (left quadrants).
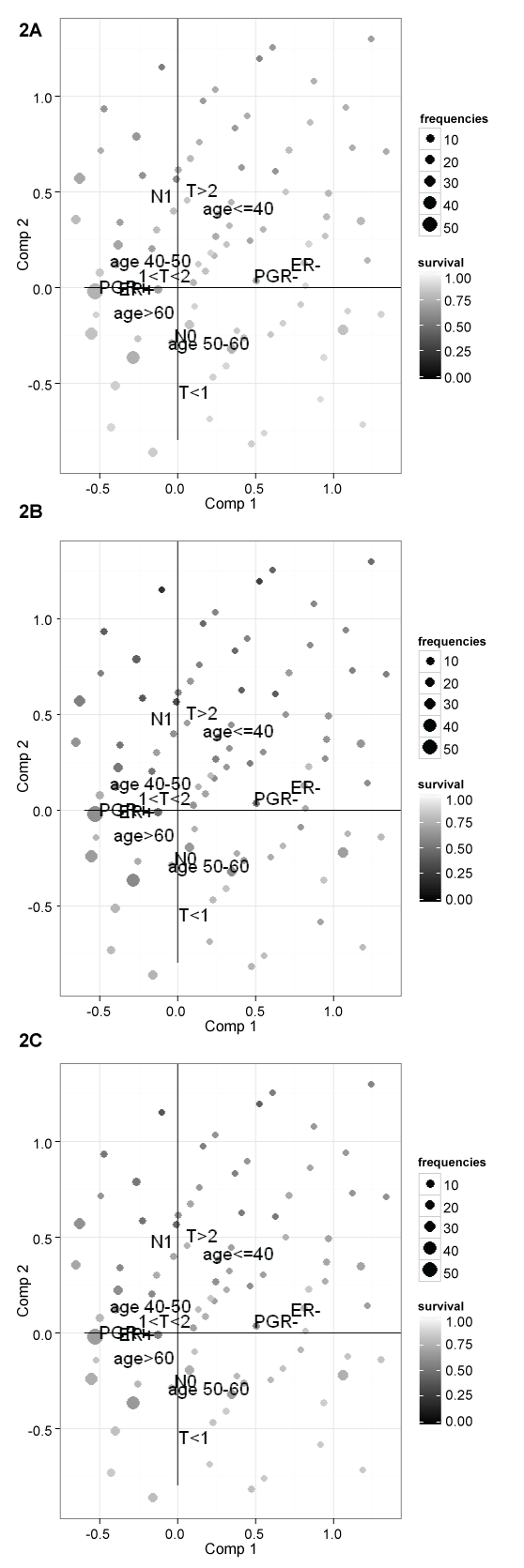
.
Figure 2: MCA plot of the pattern of the covariates together with the relapse free survival for each subject at (A) 5 years; (B) 10 years; and (C) 15 years.
View Figure 2
The net relapse free survival probability estimated for each subject at 5, 10 and 15 years are plotted as passive variables on the MCA plane (as bubbles), to describe the association with the pattern of clinical-pathological characteristics. The dimension of the bubbles are proportional to frequencies of subjects for each combination of covariates and the gray intensities of the bubble are proportional to relapse-free survival (Figure 2). It can be noted that higher risk of relapse is mainly associated with young age, lymph node metastases and pathological tumour size > 2 cm and that after 10 years of follow-up women can still experience relapse, in fact relapse free survival decreases from 5 years to 10 years and to 15 years.
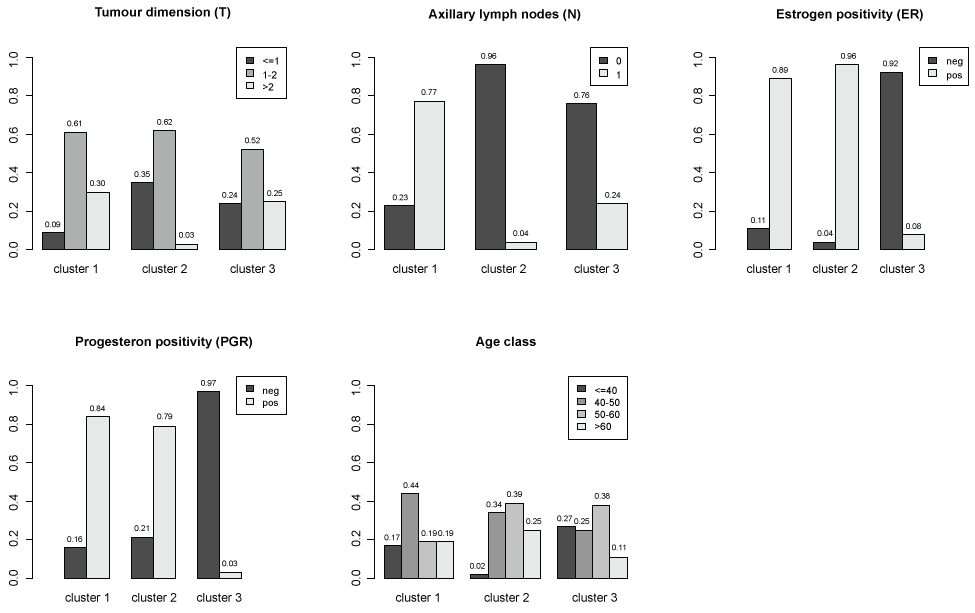
To synthesize the results of MCA and identify potential profiles of subjects sharing similar characteristics a cluster analysis is applied to the subject coordinates for first two factorial axes. Three clusters are identified. The distributions of patients characteristics within clusters are represented in figure 3. In order to better understand the relative contribution of each variable in clusters identification, a classification tree (package tree in R software) was used (Figure 4). The main characteristics of subjects in cluster 1 are: axillary lymph nodes metastases, positive estrogens receptors and tumour dimension more than 1 (117 women on 194 classified in cluster 1). The main characteristics of subjects in cluster 2 are: no axillary lymph nodes metastases, positive estrogens receptors and tumour dimension less than 2 and age more than 40 (234 women on 270 classified in cluster 2). The main characteristics of subjects in cluster 3 are: no axillary lymph nodes metastases, negative estrogens and progesterone receptors (70 women on 112 classified in cluster 3).
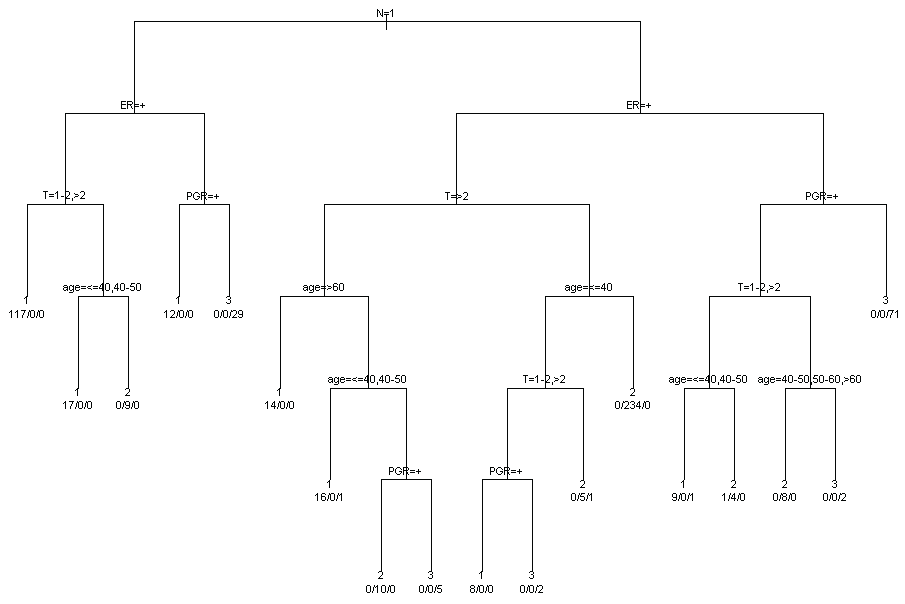
.
Figure 4: Classification tree for the joint contribution of the variables in clusters.
View Figure 4
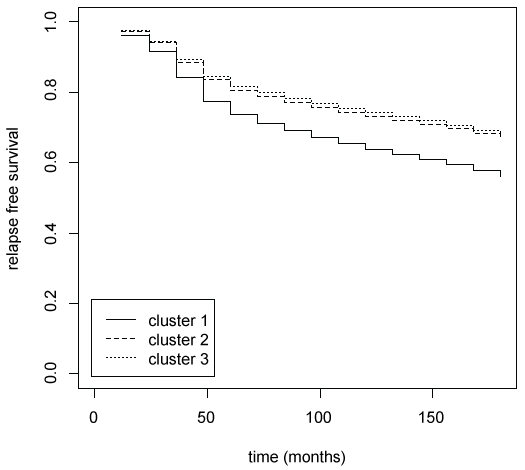
In order to summarize the prognostic results, the copula graphical estimated relapse free survival curves for each cluster are plotted in figure 5. The greater divergence is observed between cluster 1 and the other two clusters. On the contrary relapse free survival curves of clusters 2 and 3 are very similar. The main characteristics than distinguish cluster 1 and clusters 2-3 are axillary lymph nodes metastases (positive in cluster 1 and negative in clusters 2-3) and tumour dimension (bigger in cluster 1). The main characteristics than distinguish clusters 1-2 and cluster 3 are hormones receptor status (positive in clusters 1-2 and negative in cluster 3).
Discussion
To evaluate treatment or covariate effects on specific events, common regression models are based on cause specific hazards (e.g., Cox regression model) or on sub distribution hazard (e.g., Fine regression model). It can be noted that the effect of a covariate on the hazard function cannot be directly translated into the corresponding effect on the survival function (e.g. proportional hazards does not imply proportional survival probabilities) thus results do not necessarily provide useful measures of direct clinical impact as for example relative risk or odds ratio. Proposal based on Pseudo values transformational models allow to directly estimates the covariate effect on clinically useful measures [9]. However when the interest is to evaluate the covariate effect on marginal (net) survival as in the case of relapse free survival, "classical" regression model or the above mentioned transformation models for survival data do not provide direct information and specific approaches are needed. Because of the availability of partial information on multivariate time distribution some structural assumptions must be made accounting for clinical considerations which suggest the more suitable copula. Only in presence of independence among events the analysis on each event can simply performed by considering censored the times to other events.
Regression models on marginal hazard based on Archimedean copulas are available in the case of semi competing risks [19]. Dedicated software is needed and, till now, routines or functions or procedures which can be used in the widely diffuse statistical software are not available. The above mentioned papers reports in detail likelihood functions and provides some suggestions for programming but this is not a simple task. Moreover, these models are based on net hazard thus regression coefficients do not provide directly "clinically useful measures" on covariate impact on net survival.
The proposal of Lo and Wilke is an useful step to overcome the problem of difficult model implementation, although a quantification of the covariates effect of net survival cannot be obtained as happen in regression model coefficients. A limitation of their approach is the possibility to shows only the effect of each covariate one by one.
To our knowledge, an application allowing to evaluate the covariates joint effect has not been previously presented. We extended their approach to visualize the joint role of covariates on marginal survival. This is preferred since clinical covariates are often correlated. The advantages of our approach is the possibility to use standard software for all steps consisting in: a flexible estimate of marginal survival obtained by combining pseudo values model results (using formulas reported in [5]) and a multivariate technique to show joint covariate impact. MCA and cluster analysis may suggest risk groups which can be further analysed and confirmed by validation.
Acknowledgements
This work was partially funded by Institutional grant of the Italian Association for Cancer Research (AIRC) IG 2012 rif: 13420 "Statistical Tools for Prognosis and Prediction in Cancer: Assessments and Application to a Sarcoma Case Series".
References
-
Fine JP, Jiang H, Chappell R (2001) On semi-competing risks data. Biometrika 88: 907-919.
-
Kaishev, VK, Dimitrova DS, Haberman S (2007) Modelling the joint distribution of competing risks survival times using copula functions. Insurance: Mathematics and Economics 41: 339-361.
-
Nelsen RB (1999) An Introduction to Copulas. Springer, New York.
-
Marubini E, Valsecchi MG (1995) Analysing Survival Data from Clinical Trials and Observational Studies. John Wiley and Sons, Chichester.
-
Lo SMS, Wilke RA (2014) A regression model for the copula graphic estimator. Journal of Econometric Methods 3: 21-46.
-
Lakhal L, Rivest LP, Abdous B (2008) Estimating survival and association in a semicompeting risks model. Biometrics 64: 180-188.
-
Xu J, Kalbfleisch JD, Tai B (2010) Statistical analysis of illness-death processes and semicompeting risks data. Biometrics 66: 716-725.
-
Andersen PK, Klein JP, Rosthøj S (2003) Generalised linear models for correlated pseudo-observations, with applications to multi-state models. Biometrika 90: 15-27.
-
Ambrogi F, Biganzoli E, Boracchi P (2008) Estimates of clinically useful measures in competing risks survival analysis. Stat Med 27: 6407-6425.
-
Clayton DG (1978) A model for association in bivariate life tables and its application to epidemiological studies of familial tendency in chronic disease epidemiology. Biometrika 65: 141-151.
-
de Uña-Álvarez J, Veraverbeke N (2013) Generalized copula graphic estimator. Test 22: 343-360.
-
Kalbfleish JD, Prentice RL (2002) The Statistical Analysis of Failure Time Data. (2nd edn), John Wiley and Sons, Hoboken, New Jersery.
-
Harrell FE, Lee KL, Mark DB (1996) Tutorial in biostatistics multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in medicine 15: 361-387.
-
Husson F, Lê S, Pagès J (2010) Exploratory multivariate analysis by example using R. CRC press.
-
Greenacre M, Blasius J (2006) Multiple correspondence analysis and related methods. CRC Press.
-
Biganzoli E, Boracchi P, Coradini D, Daidone MG, Marubini E (2003) Prognosis in node-negative primary breast cancer: a neural network analysis of risk profiles using routinely assessed factors. Annals of oncology 14: 1484-1493.
-
Mariani L, Salvadori B, Marubini E, Conti AR, Rovini D, et al. (1998) Ten year results of a randomised trial comparing two conservative treatment strategies for small size breast cancer. Eur J Cancer 34: 1156-1162.
-
Veronesi U, Marubini E, Mariani L, Galimberti V, Luini A, et al. (2001) Radiotherapy after breast-conserving surgery in small breast carcinoma: long-term results of a randomized trial. Ann Oncol 12: 997-1003.
-
Peng L, Fine JP (2007) Regression modeling of semicompeting risks data. Biometrics 63: 96-108.