While in circulation, red blood cells (RBC) need to elastically undergo large deformations without lysing, an ability that may be compromised by cell membrane damage. Such can be tested in vitro by subjecting an RBC sample to external mechanical stress, e.g. through bead milling or oscillation of an object in a sample. In addition to controlling frequency and duration of oscillations, this approach can be further tailored by bead selection/design.
This work studies effects of different beads in creating qualitatively as well as quantitatively different shear stresses when oscillated in a sample containing RBC.
Identical, diluted RBC samples were stressed via bead milling using different beads, with hemolysis profiles developed in each case.
Bead dimensions significantly impacted induced stress, both in magnitude as well as type, as reflected by hemolysis under respective conditions. Specifically, cell protection (from lysis) afforded by albumin (when present in the medium) showed a complex dependence on bead length and diameter, with the effect seemingly indicative of multiple combined stresses induced by the bead oscillation. The effect is described as an interplay of stresses generated in bead wake in combination with those generated in the annulus.
Bead oscillation based mechanical fragility (MF) profiling of RBC presents a useful tool for exploring effects of different shear stress types for various potential applications for assessment of blood damage, and particularly of sub-hemolytic red cell damage.
Red blood cell(s), RBC, Erythrocyte, Mechanical fragility, Bead milling, Shear stress, Hemolysis
While in circulation, red blood cells (RBC) need to elastically undergo large deformations while passing through the capillary network, without lysis (rupture), and even larger deformation when passing through spleen inter-endothelial slits. This ability is mediated by the cell plasma membrane, the only structural element of RBC, which is composed of a lipid bilayer linked by transmembrane protein complexes (notably Band 3-ankyrin and 4.1R) to spectrin elastic network. It has been suggested that overall membrane cohesion may be determined by these bilayer-skeleton linkages, mainly by those mediated by Band 3. On the other hand, mechanical stability of the RBC membrane seems to be determined primarily by the proteins associated with 4.1R complex, with 4.1R protein and actin having the biggest influence, as well as by spectrin-spectrin. Membrane deformability, defined as the extent of stress-induced deformation of the cell membrane without lysis, and membrane stability, defined in that case as the maximum extent of deformation before the cell fails to recover its shape, were shown to depend on different membrane skeletal protein interactions, and thus can change without a fixed relationship to each other (upon RBC membrane perturbations) [1].
External mechanical stress can potentially induce different types of deformation in the RBC membrane, including compression-stretching (associated with changes in membrane area), bending (and/or torsional) deformations, and shear deformations that do not affect changes in RBC surface area (which would not necessarily preclude local perturbations of the spectrin network, associated for example with redistribution of anchor protein complexes).
Such perturbations, manifested as changes to membrane components, can result in reduced mechanical stability of RBC. That, in turn, leads to accelerated cell fragmentation and hemolysis, which, besides anemia, was implicated in a cascade of detrimental events associated with the release of hemoglobin (e.g. [2]). Membrane modifications can also arise through various pathologies and diseases, blood storage, or the action of drugs or blood-contacting devices. While RBC may exhibit high apparent tolerance to fluidic shear stresses, cells can be altered even when such stress does not reach the hemolytic threshold. Such "sub-hemolytic" damage may lead to later hemolysis in circulation, in addition to any other potential impairment of cell function.
The membrane property of mechanical fragility (MF) defines cells' ability to withstand applied mechanical stress without rupturing (lysing), and is dependent on a variety of cellular attributes, including, among others, intracellular viscosity, membrane viscoelasticity and interaction of lipid bi-layer with cytoskeleton [3] - properties that are not necessarily uniformly affected by external stress. It is considered to be a sensitive indicator of sub-hemolytic RBC damage - blood trauma not resulting in direct or overt hemolysis, but nevertheless leading to a shortened RBC life span in circulation [4]. One approach to measure MF is a rocker-bead test that involves slow rocking of a blood vial containing a stainless steel ball (bead) for a predetermined time [5]. Another approach involves 20-50 Hz oscillations of a stainless-steel ball, with the development of a MF profile, reflecting observed levels of induced hemolysis (e.g., from zero to a hundred percent) over the total duration of oscillations [6].
It had been demonstrated previously that for a sphere/ball, hemolysis is caused predominantly by wake turbulence, with presumably ball speed (related to oscillation frequency) and viscosity affecting the nature of turbulence in the medium [7]. Then, an additional ability to vary the type(s) of hemolysis-inducing stress was introduced, regarding when the spherical bead is replaced with a cylindrical bead design [8]. Such cylindrical beads, oriented longitudinally in a tubular container, can introduce annular flows, with the length of the annulus depending on the bead's length, and the gap thickness depending on the relative diameters of the bead and tube. That presents not only a potentially different flow type within the annulus itself, but also potentially much more cell interaction at the solid surface interface (bead annulus surface). Preliminary results suggested that with cylindrical beads, in addition to effects of wake turbulence, induced hemolysis is also affected by two kinds of annular effects - tentatively associated with in-bulk and surface-related causes. It was shown that changes in bead geometry could be used to vary relative contributions of different types of stress in the sample. That opens the possibility of being able to perturb different structural components of the RBC membrane to different respective and controlled extents, thus allowing more targeted probing of membrane response to mechanical stress and resultant hemolysis and sub-hemolytic RBC damage [8]. The present work aims to further expand the understanding of factors influencing mechanically induced hemolysis of RBC when cylindrical beads are used to induce quantitatively and qualitatively different fluidic stresses, as well as to explore how such stresses' relative proportions and/or interplay could potentially be used to probe membrane condition (perhaps sufficiently resembling, or at least reflecting, components of relevant physiological stresses).
Blood components (packed RBC or pRBC, and Fresh Frozen Plasma or FFP) were obtained from American Red Cross Biomedical Services and stored according to AABB Standards [9]. Bovine Serum Albumin was purchased from Sigma-Aldrich (St. Louis, MO) and RPI Corp (Mt. Prospect, IL). Mechanical Fragility (MF) testing and profile development was performed using a vertically oscillating bead in a sample and having incremental hemolysis being measured at respective stressing durations, as was described previously [7], except now using custom made cylindrical beads in addition to the standard spherical (ball) beads. Area Under the Curve (AUC), representing the area under the collected fragility profile, is a profile-based value that was used here to evaluate induced hemolysis over a given aggregate stress duration. Bead speeds during oscillation were measured through analysis of video recordings of bead movement in the bead mill used in the experimental conditions. Records of bead movement were obtained using a high-speed camera (Casio Exilim HS, Casio, Yamagata, Japan) used in 240-520FPS mode. Image analysis was performed by Tracker 4.92, an open source video analysis and modelling tool (Douglas Brown, 2016). Bead speed was calculated from the distance the bead travelled through the medium over a given time interval. Average bead speed is based on recordings of 3 to 5 seconds of bead movement. Data is presented in the form of sample mean and standard deviation (SD), the median, with 1.5 × IQR (interquartile range) where appropriate. One sample Student t-test or signed rank test with a two-tailed p-value of 0.05 was used to test for statistical significance. Fits shown on the figures are for illustration purposes only. Additional details regarding this section are provided in a Supplement.
Dependence of induced hemolysis on the length of the bead in AS3 media, supplemented and not supplemented with albumin (Figure 1), shows a maximum at about 22 mm, corresponding to about a 0.6 bead-length to tube-length ratio (RBL/TL). With a small cylindrical bead (7 mm in diameter, and 6 or 7 mm in length), unlike when a 7 mm sphere was used, albumin supplementation did not result in a decrease in induced hemolysis. A reverse effect, elevated hemolysis, was instead reproducibly observed (Figure 1, Insert A). For longer cylinders, medium supplementation with albumin did result in a sharp decline in observed hemolysis. The magnitude of this protective effect was maximal for beads of 20 mm in length (~ 0.55 RBL/TL; Figure 1, Insert B). When normalized to induced hemolysis observed in AS3 un-supplemented media, the maximum effect remains at 18-20 mm bead length, although the dependency relationship becomes less sharp (not shown).
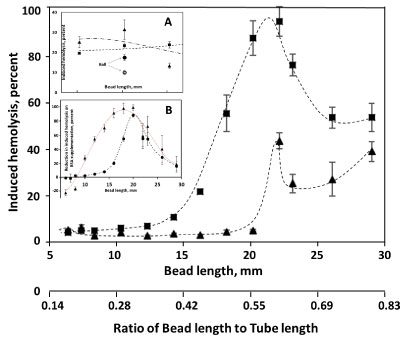 Figure 1: Dependence of induced hemolysis on the length of the bead used. Cylindrical beads, with the diameter of 7 mm and having different lengths, were oscillated at 30 Hz in 500 μl of AS3 solution with (▲) and without ( ■ ) supplementation with 4 g/L BSA. Shown is induced hemolysis after 3 min of stress application (recalculated from 10 min of stress application for beads shorter than 18 mm). Insert A shows the induced hemolysis in the same experiments with beads 6-8 mm length after 15 min of stress application (with (▲) and without ( ■ ) albumin supplementation), in comparison with a 7 mm diameter spherical bead with (○) with without (●) supplementation with BSA. Insert B shows the difference between hemolysis in AS3 media induced without BSA and that containing 4 g/L BSA(- - ● - -), and KBSA, the same difference normalized to the amount of hemolysis observed in non-supplemented AS3 (···▲···). "Fits" are for illustration purpose only.
View Figure 1
Figure 1: Dependence of induced hemolysis on the length of the bead used. Cylindrical beads, with the diameter of 7 mm and having different lengths, were oscillated at 30 Hz in 500 μl of AS3 solution with (▲) and without ( ■ ) supplementation with 4 g/L BSA. Shown is induced hemolysis after 3 min of stress application (recalculated from 10 min of stress application for beads shorter than 18 mm). Insert A shows the induced hemolysis in the same experiments with beads 6-8 mm length after 15 min of stress application (with (▲) and without ( ■ ) albumin supplementation), in comparison with a 7 mm diameter spherical bead with (○) with without (●) supplementation with BSA. Insert B shows the difference between hemolysis in AS3 media induced without BSA and that containing 4 g/L BSA(- - ● - -), and KBSA, the same difference normalized to the amount of hemolysis observed in non-supplemented AS3 (···▲···). "Fits" are for illustration purpose only.
View Figure 1
In the vertical bead mill employed for this work, it is the head of the mill, with the sample tubes inside, that is actually (directly) oscillated. Thus, the bead's actual movement is determined by a combination including drag forces as the fluid medium around the bead shifts in response to the tube's oscillation, fluid resistance to bead movement, and gravity. The bead's range of the movement is constrained by the top and the bottom of the tube. Shear stress arises due to displacement of the tube and the media therein relative to the bead, and thus the term "bead movement" in this context should be understood to encompass a bead's displacement relative to the oscillating tube (within the oscillating tube holder), with "bead speed" - as an absolute value of bead velocity relative to the oscillating tube - thus representative of the speed of the medium's movement relative to the bead. As all beads here are simple cylinders or a sphere, direction of the flow over the bead, and thus the direction of the bead travel (up or down), should not affect the resultant induced hemolysis. Thus, a scalar value of speed is presented, instead of velocity, which is a vector quantity.
When evaluated using a high-speed camera, bead movement was found to be markedly uneven over the course of oscillations (Figure 2). No significant bead "loitering" at one or the other end of the tube had been observed at any oscillating frequencies, although all beads, regardless of their length, reached both ends on the tube. While longer beads (over 18 mm in length) reached both ends at each oscillation, that was not the case for shorter beads, with very short beads (e.g. 6-7 mm cylindrical beads, or 7 mm ball, Figure 2) reaching the end of the tube only occasionally. For shorter beads, the overall movement appeared to occur with a low frequency oscillation (e.g. 7-8 Hz for a 6-7 mm cylindrical bead), overlaid with a higher frequency 30 Hz oscillations - same as the oscillation frequency of the bead mill, and thus of the sample tube. Similar effect was observed at other oscillation frequencies in the 20-50 Hz range. With increased bead length, the frequency of the low frequency component appeared to increase (12 mm bead, Figure 2); however, its overall contribution to the bead's movement declined. Longer beads, relative to the tube length (20 mm in length and longer; RBL/TL ≥ 0.55), exhibited only the high frequency oscillation, that of the bead mill and the sample tube (20 mm bead, Figure 2). While variability in bead speed during bead milling was anticipated, as it is an inherent attribute of that method, the significant non-regularity in shorter bead movement was unexpected.
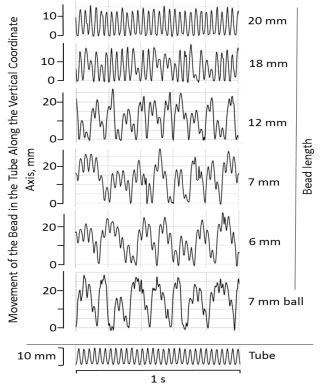 Figure 2: Vertical oscillation of sample-containing tube and of the beads of different length in the tube (movement of a bead relative to the sample) over a 1 second time interval. Conditions as in Figure 1.
View Figure 2
Figure 2: Vertical oscillation of sample-containing tube and of the beads of different length in the tube (movement of a bead relative to the sample) over a 1 second time interval. Conditions as in Figure 1.
View Figure 2
Dependence of average bead speed on bead length is shown in Figure 3, with the box-and-whiskers plot of the speed distributions given in the insert. Notably, average speeds and speed distributions were found to be similar for a ball and for cylindrical beads of a comparable size. Overall, on average, increased length up to about 20 mm (0.55-0.6 bead/tube length ratio), resulted in faster bead movement, and after that threshold, bead speed declined. Supplementation with albumin resulted in an about a 20 percent decrease in average speed for beads 18-23 mm in length, with the difference declining for beads both longer and shorter, with essentially no difference observed for very short (6-8 mm in length) beads.
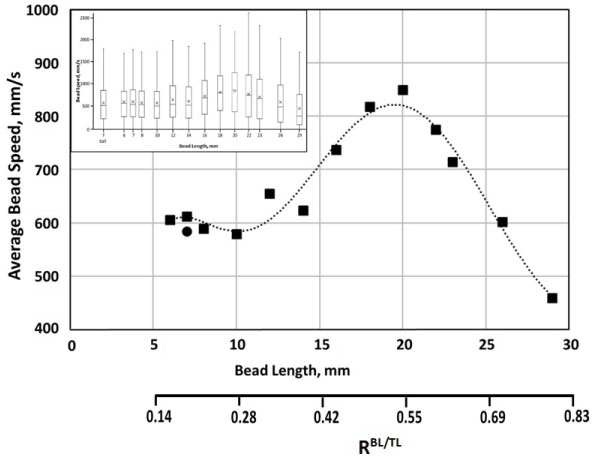 Figure 3: Dependence on the average speed (absolute velocity), of 7 mm in diameter cylindrical beads in AS3 solution, on the bead's length (■). Also shown is the average speed of a 7 mm sphere/ball in the same conditions (●). Insert contains a box-and-whiskers plot of speed distribution, with the box showing upper and lower quartiles, the median, and the mean (X), and lower and upper whiskers showing 1.5 x IQR (interquartile range). Trends, shown by dashed lines (- - -), are for illustrative purpose only. Conditions as in Figure 1.
View Figure 3
Figure 3: Dependence on the average speed (absolute velocity), of 7 mm in diameter cylindrical beads in AS3 solution, on the bead's length (■). Also shown is the average speed of a 7 mm sphere/ball in the same conditions (●). Insert contains a box-and-whiskers plot of speed distribution, with the box showing upper and lower quartiles, the median, and the mean (X), and lower and upper whiskers showing 1.5 x IQR (interquartile range). Trends, shown by dashed lines (- - -), are for illustrative purpose only. Conditions as in Figure 1.
View Figure 3
Bead diameter was another factor affecting the magnitude of induced hemolysis (Figure 4). The dependence was complex, and at all oscillated frequencies used (from 20 to 50 Hz), in non-supplemented media, it exhibited an increase for bead diameters from 5.5 mm to 6 mm, corresponding to an increase in bead to tube diameter ratio (RBD/TD) from ab. 0.6 to ab. 0.7. That corresponded to a small, but reproducible, increase in observed hemolysis. Similarly, at all frequencies, induced hemolysis was minimal for beads 7 mm in diameter (RBD/TD ≈ 0.8). Magnitudes of induced hemolysis rapidly increased for larger diameter beads (up to 8 mm, RBD/TD ≈ 0.9). Such an increase was more pronounced at 50 Hz than at any of the lower frequencies (Figure 4; 40 Hz results are shown for comparison). Supplementation of media with albumin resulted in lessening of induced hemolysis, with the magnitude of such protection also varying with bead diameter (Figure 5). This dependence was in general similar to that observed in non-supplemented media, particularly at lower oscillation frequencies. At 50 Hz, the minimum (for induced hemolysis dependence, in the presence of albumin,on bead diameter) observed for 7 mm beads (RBD/TD ≈ 0.8) is sharper, and the increase in hemolysis when larger diameter beads are used is markedly more pronounced (Figure 4). As a result, at this frequency, for beads over 7 mm in diameter, supplementation with albumin provided progressively smaller protection against induced hemolysis. Notably, the magnitude of these effects varied between different RBC samples, with some exhibiting a larger impact of supplementation than others (Figure 4).
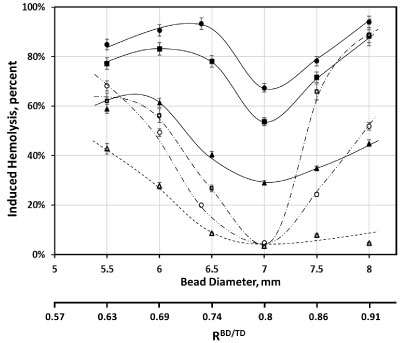 Figure 4: Dependence of induced hemolysis on the diameter of a bead. Cylindrical beads, 18 mm in diameter, were oscillated at 50 Hz for 2 minutes in 950 μL of AS3 solution, with (□; ○ for an alternative RBC sample) and without (■;● for an alternate RBC sample) supplementation with 4 g/L BSA, and at 40 Hz for 4 minutes, with (Δ) and without (▲) albumin supplementation. Fits are for illustrative purposes only; solid lines are for non-supplemented data, and dashed are for that involving supplementation with albumin; oscillation was at 50 Hz (- ∙ - ∙ -, and - ∙∙ - ∙∙ - for alternative RBC sample) and at 40 Hz (- - -).
View Figure 4
Figure 4: Dependence of induced hemolysis on the diameter of a bead. Cylindrical beads, 18 mm in diameter, were oscillated at 50 Hz for 2 minutes in 950 μL of AS3 solution, with (□; ○ for an alternative RBC sample) and without (■;● for an alternate RBC sample) supplementation with 4 g/L BSA, and at 40 Hz for 4 minutes, with (Δ) and without (▲) albumin supplementation. Fits are for illustrative purposes only; solid lines are for non-supplemented data, and dashed are for that involving supplementation with albumin; oscillation was at 50 Hz (- ∙ - ∙ -, and - ∙∙ - ∙∙ - for alternative RBC sample) and at 40 Hz (- - -).
View Figure 4
Progressively increased diameter of the bead resulted in a linear decline in bead average speed, likely due to increasing resistance of the medium, which would be negatively correlated with the bead cross-section (Figure 5). Such decline was observed in both albumin-supplemented and non-supplemented AS3 media.
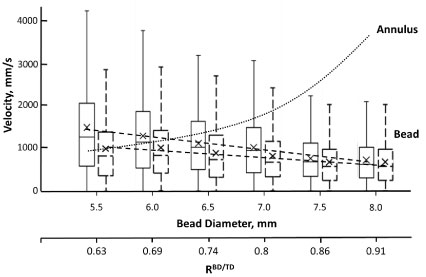 Figure 5: Box and whiskers plot of the dependency of the average velocity of 18 mm length cylindrical beads on the bead's diameter, when oscillated at 50 Hz, in AS3 medium (solid line plots) and in BSA-supplemented medium (dashed line plots). Dotted line (∙∙∙∙∙∙) illustrates calculated changes in annulus flow speed for the same beads (results shown for beads in AS3 medium). Conditions as in Figure 4.
View Figure 5
Figure 5: Box and whiskers plot of the dependency of the average velocity of 18 mm length cylindrical beads on the bead's diameter, when oscillated at 50 Hz, in AS3 medium (solid line plots) and in BSA-supplemented medium (dashed line plots). Dotted line (∙∙∙∙∙∙) illustrates calculated changes in annulus flow speed for the same beads (results shown for beads in AS3 medium). Conditions as in Figure 4.
View Figure 5
Bead weight was found to be a factor significantly affecting induced hemolysis (Figure 6), with the increased weight corresponding to higher hemolysis in both un-supplemented and supplemented-with-albumin media. In all cases, higher weights were also associated with higher average bead speeds (Figure 6).
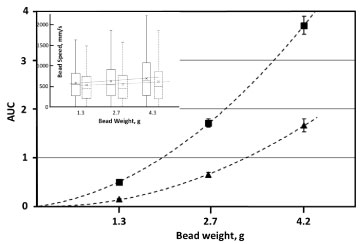 Figure 6: Dependence of induced hemolysis on the weight of a bead. Cylindrical beads, 7 mm in diameter and 14 mm in length, were oscillated at 30 Hz for up to 10 minutes in 350 μL of AS3 solution, with (▲) and without ( ■ ) supplementation with 4 g/L BSA. Induced hemolysis is represented as AUC of the hemolysis profiles. Insert contains a box-and-whiskers plot of speed distribution, with elements defined as in Figure 3. Shown are the results with ( - - - ) and without ( ⸺ ) medium supplementation with 40 g/L albumin. Linear "fits" are for illustrative purpose only.
View Figure 6
Figure 6: Dependence of induced hemolysis on the weight of a bead. Cylindrical beads, 7 mm in diameter and 14 mm in length, were oscillated at 30 Hz for up to 10 minutes in 350 μL of AS3 solution, with (▲) and without ( ■ ) supplementation with 4 g/L BSA. Induced hemolysis is represented as AUC of the hemolysis profiles. Insert contains a box-and-whiskers plot of speed distribution, with elements defined as in Figure 3. Shown are the results with ( - - - ) and without ( ⸺ ) medium supplementation with 40 g/L albumin. Linear "fits" are for illustrative purpose only.
View Figure 6
When bead oscillation is used to induce hemolysis, as can be expected, an increase in oscillation frequency results in increased hemolysis. In this case, oscillation frequency determines the periodicity of oscillations (e.g., as shown for 30 Hz frequency on Figure 2); however, such periodicity is not the only factor determining the amount of induced hemolysis. Increase in oscillation frequency here is also associated with increased speed of the bead relative to the medium in the sample tube (data not shown), thus potentially affecting the intensity of induced hemolysis. (Here, intensity of hemolysis is defined as the amount of hemolysis induced per oscillation. Figure 7 presents the intensity as hemolysis per 1 minute of stress application per 1 Hz, thus, for each frequency, showing average hemolysis resulting from 60 periods of oscillation). Figure 7 shows the intensity of hemolysis induced by 7 and 18 mm-long beads at frequencies from 15 to 50 Hz.
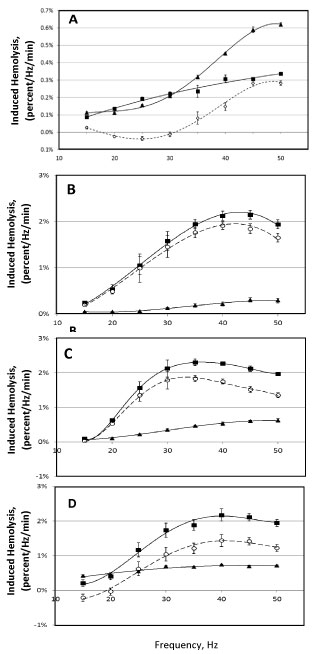 Figure 7: Dependence of induced hemolysis on the oscillation frequency of the bead mill. Hemolysis was induced using cylindrical beads 7 mm in diameter and 7 mm long, oscillated for 3-10 min in 350 μL sample volume (A); and 18 mm-long beads, oscillated for 1 min in 500 μL sample volume (B-D). Medium is AS3, with (▲) and without ( ■ ) supplementation with 4 g/L BSA, with the difference shown by open symbols ( ◯ ). Packed RBC sample was 9 (B), 45 (C) and 65 (D) days post-collection. (An apparent decrease in hemolysis in un-supplemented AS3 at high frequencies, e.g. 40-50 Hz for 18 mm beads, is an artefact of normalization due to saturation effect, when hemolysis begins to approach 100 percent).
View Figure 7
Figure 7: Dependence of induced hemolysis on the oscillation frequency of the bead mill. Hemolysis was induced using cylindrical beads 7 mm in diameter and 7 mm long, oscillated for 3-10 min in 350 μL sample volume (A); and 18 mm-long beads, oscillated for 1 min in 500 μL sample volume (B-D). Medium is AS3, with (▲) and without ( ■ ) supplementation with 4 g/L BSA, with the difference shown by open symbols ( ◯ ). Packed RBC sample was 9 (B), 45 (C) and 65 (D) days post-collection. (An apparent decrease in hemolysis in un-supplemented AS3 at high frequencies, e.g. 40-50 Hz for 18 mm beads, is an artefact of normalization due to saturation effect, when hemolysis begins to approach 100 percent).
View Figure 7
While movement of the 18 mm-long bead, at all frequencies, can be described as essentially oscillations from one end of the tube to the other end, the 7 mm bead, at each oscillation, traverses only a small distance through the tube, and thus through the medium, and with an overall movement that is much more erratic and complex than that for the longer beads. Despite this difference, for both beads, increase in oscillation frequency results in more pronounced protection against hemolysis (being afforded by albumin). In some cases, at low frequencies, albumin supplementation not only failsto protect RBC against this type of mechanical stress, but even appears to be detrimental to RBC stability (here, resistance to lysis) under stress (Figure 7A and Figure 7C). While this effect was commonly observed when 7 mm-long beads were used, it was also observed with "expired" (over 42-days-old) stored pRBC. Figure 7A, Figure 7B and Figure 7C illustrate the changes observed in a given packed RBC sample when tested repeatedly at 9, 46, and 65 days post-collection. It should be noted that the magnitudes of those effects were not only affected by storage time, but also varied for blood samples from different donors. In particular, some "fresh" (under 14 days in storage) packed RBC samples did not exhibit any statistically significant changes in induced hemolysis at low (15-20 Hz) oscillation using either 7 or 18 mm long beads upon supplementation with albumin. The reasons underlying this variability remain to be investigated.
As indicated, the specific means of stressing the RBC in MF testing can qualitatively affect the results. For example, it had been demonstrated that albumin supplementation of the medium can "protect" RBC against certain types of mechanical stress such as certain bead oscillation approaches [7,10], yet not with some alternative methods (e.g., a jet/orifice system [11]). It was also found that, even within bead milling with spherical beads, at least some changes in the magnitude of the protective effect afforded by albumin can be attributed to changes in properties of turbulent flows in the bead's wake [7].
Furthermore, use of a cylindrical (rather than spherical) bead introduces additional stresses, beyond those of the bead's turbulent wake, associated with the bead's annulus (which is notably minimal in the case of a spherical bead). Those would be related both to the flow through the annulus and to the increased opportunity of cell interaction with the bead's annular surface. (Note that in the configuration here, the interaction with the bead's surface is of primary relevance, as the medium remains largely stationary relative to the enclosing tube's wall). Such stresses can, as was shown previously [8], and as confirmed in this work, significantly modify magnitudes both of induced hemolysis and of the protection from it due to media supplementation with albumin.
The dependence of induced hemolysis on bead geometry was complicated, and at least in part was found to depend on bead speed. Bead movement within the tube and through the medium is determined through the interplay of flow drag and flow resistance forces, combined with the effect of gravity and with direct bead impact with the oscillating tube (within the bead mill head or tube-holder). Over each oscillation period, bead speed and thus flow speed around the bead would be continuously changing, with the speed distribution as for example shown on inserts in Figure 3, Figure 5 and Figure 6. Thus, over each oscillation period, RBC would be subject to changing levels of mechanical stress. In the present work,we directly determined the bead speed throughout oscillations (via video) and attempted to represent the impact of speed through average speed values. Such approach has clear limitations, and future attempts of linking induced hemolysis directly with distribution profiles could potentially provide additional insight into mechanisms of cell damage.
There is a striking similarity between the induced hemolysis and average bead speed dependencies on bead length (Figure 1 and Figure 3). For RBL/TL < 0.6, the increase in bead speed with increased bead length is likely due to the progressively increasing bead weight (per Figure 6), even though offset by the increased flow resistance, which likely increases linearly with the length of a bead. It should be noted, that the dependence of bead speed on its length, and the dependence of resultant hemolysis on bead's length, are not a simple (linear) function of the weight and the length of a bead. Normalization for these parameters (assuming linear dependence) does not produce a uniform (per unit of weight and/or length) hemolysis (data not shown). That implies either a higher order function of weight/length dependence or a more complex dependence, which could involve other (e.g., medium related) parameters changing along with (for example) the bead's length change.
For RBL/TL > 0.6,the bead's speed and the associated hemolysis decline is likely due to bead movement being constrained by the length of the tube, which imposed a limit on how far a bead may travel during each oscillation. That is supported by the pattern of bead movement recorded by high-speed camera, which shows that for beads 20 mm and longer, the bead oscillates between the ends of the tube with the frequency of the tube oscillation (Figure 2). (Note that this was not the case for shorter beads, which exhibited a random-movement behavior, rarely reaching the ends of the tube, as demonstrated by the ranges of bead movement). Thus, constrained by the tube, longer beads would not be able to reach velocities that would be otherwise expected, with bead velocity approaching zero when RBL/TL is approaching 1. Note that for some bead and tube geometries as well as stress application parameters (e.g. oscillation frequency and intensity), increasing the length of the cylindrical bead could result in decreased speed of the bead's movement in the tube (possibly due toa lower final speed for each oscillation, which in turn may be a function of decreased opportunity for acceleration). This could lead to a more complex manifestation of albumin's protective effect (e.g. a decrease in the effect followed by an increase) with increasing bead length, reflecting changes in the overall composition of mechanical stress types being applied to RBC. Such complex dependencies still require further investigation.
Average velocities of movement through the media were similar between short (6-7 mm in length) cylindrical beads and a spherical bead of comparable diameter (7 mm), implying potentially similar wake turbulence and thus hemolysis associated with wake turbulence. For such beads overall hemolysis magnitudes were indeed comparable in non-supplemented AS3, but not in albumin supplemented media (Figure 1). The results suggest the existence of at least two hemolysis inducing effects that depend on bead length: One for which albumin makes cells more susceptible to hemolysis, and another, where,with increased bead length, albumin provides progressively greater protection against hemolysis - supporting conclusions drawn previously [8].
With just spherical beads, it had been demonstrated that effectiveness of protection against hemolysis, provided by albumin, depends on the speed of the bead, possibly due a transition of Von Karman trail to a progressively more disorganized wake [7]. The scale of protection against shear stress, and thus cell hemolysis, can be evaluated using an albumin protection coefficient, where is induced hemolysis in non-supplemented media and is hemolysis in media supplemented with albumin. In that study, the changes of average bead speed from 450 to 1,300 mm/s mm per sec was associated with a 50 percent increase in KAlbumin. (There, the changes in bead speed were the result of changes in oscillation frequency between 20 and 50 Hz).
However, as shown here, for small cylindrical beads KAlbumin is negative, and changes in bead length resulted in much smaller changes in average speed (from ~600 to ~800 mm/s); however, it was associated with much more pronounced changes in KAlbumin, from negative 27 percent for a 6 mm long bead to about + 95 percent for a 20 mm long bead. These observations indicate that speed-associated changes in wake turbulence are unlikely to drive bead-length related changes in how albumin supplementation affects hemolysis.
It is more likely that such effects are associated with the annulus - e.g., a bulk annulus flow stress (possibly with increased flow laminarity due to turbulence suppression [12]), combined with stress due to RBC interaction with the bead annulus surface (possibly similar to a phenomenon discussed previously [13]).
The speed of the annular flow (medium flow relative to the bead's surface) depends on the speed of the bead itself and on the ratio of cross-sections of the tube and the bead. At constant bead diameter (if only the bead length is changing between tests this ratio remains constant, making the speed of annulus flow linearly dependent on the bead's speed, with faster annular flow for faster moving beads. That is no longer true when the diameter of the bead is no longer constant between beads. For beads used in this work, an increase in diameter, and thus in RBD/TD, resulted in progressive linear decrease in measured bead speed (Figure 5). However, the speed of annulus flow would increase nearly exponentially with an associated decrease in annular opening cross-section. Note that while bead weight by itself would be positively correlated with bead speed, in this case, this effect is apparently secondary to a concurrently increasing flow resistance due to increase in bead diameter and smaller annular opening.
Thus, initial decline in the magnitude of induced hemolysis with increase in bead diameter (up to RBD/TB = 0.8) would most likely be associated with a decline in wake turbulence due to decreasing speed of the bead. Follow up increase in induced hemolysis could be due to exponential increase in annular flow rate and associated annulus-related stresses. That implies a marked shift in relative contributions of the stresses with the changes in bead diameter, and in the resultant contribution of annulus-associated stresses to overall cell hemolysis.
RBC response to mechanical stress had been previously evaluated using a variety of methods, including capillary or tube flow, jets, rotational disks and concentric cylinders, cone and plate arrangements, and bead(s) oscillation or agitation [11,14-19]. Hemolysis was observed both in-bulk (including cell-cell and direct shear) and at solid surface and air interfaces (e.g. [20-22]), with the material of the blood-contacting surface potentially able to influence RBC damage (e.g. [13,23]). Both laminar and turbulent flows had been implicated in cell fragmentation with different hemolytic thresholds and mechanisms of flow-induced hemolysis [15,22,24]. In laminar flows, the stress across the membrane would be determined by the flow around the cell and relate to velocity gradient and fluid viscosity. In turbulent flow, additional stress would relate to chaotic eddy motion, when Kolmogorov scale approaches the scale of RBC. There the stress would depend on the actual properties of the turbulence, with large eddies transporting cells and resulting in low stress gradient across the cell, and thus low actual stress on the cell membrane. Small (compared to the cell size) eddies could, on the other hand, create large velocity gradients across the membrane, resulting in significant stress. Thus, it was suggested that cell damage in turbulent flow arises only through eddies comparable to cell size (described through the Kolmogorov length scale) [25,26]. Such effects cannot be predicted from Reynolds stress alone, as Reynolds stress does not account for potential variability in scale sizes.
Experimentally, in-bulk hemolysis would have two main determinants: Shear stress intensity/level and exposure time. Cells can, for a short time, withstand very high stress, with prolonged exposure leading to hemolysis at a much lower stress levels, and no hemolysis occurring below a certain, even lower, stress threshold [20,27,28]. RBC ability to withstand applied mechanical stress was also shown to be markedly affected by cell environment [7,10]. Overall, the relative contribution of factors leading to stress-induced hemolysis would vary between various experimental setups and regimes of testing, with each case potentially giving predominance to a unique combination of factors.
Depending on the type of flow and the shear rate, RBC can exhibit a variety of dynamic states including rolling, tumbling and Fies by-like swinging [29]. Chaotic motion is also possible especially in a turbulent flow. Commonly described is a "tank treading", which portrays a tank-thread-like rotation of the cell membrane around the cytoplasm. Incidentally, tank treading had been shown to result in a RBC concentration gradient, with cells disproportionally concentrated towards the center of the blood vessel [30]. (Such could conceivably occur within the bead's annulus in the case of a sufficiently laminar flow).
The type of impact due to the flow can potentially be described through Reynolds numbers, which for oscillating beads, would likewise oscillate, due to the constantly changing speed of the bead and thus of the flow over the bead. Moreover, for cylindrical beads, flow dynamics and Reynolds numbers would be expected to differ between bead wake and annulus flow.
For cylindrical beads of given diameters, a change in a bead's length would impact Reynolds numbers for both wake and annulus flows, as both would be primarily impacted by the changes in bead speed. Accordingly, in both cases, estimated R values were highest for 18-20 mm beads and lowest for the 29 mm bead (Table 1). For the geometry used in this work, average Re values for annular flow would be lower than for the wake flow, as increased flow speed through the annulus is compensated by the decrease in the hydraulic diameter. Supplementation with albumin resulted in increased density and dynamic viscosity of the medium, and associated reduction in bead speed, with overall lower Reynolds numbers for both wake and annulus flows (Table 1). (It should be noted that while average Re values allow for an approximate analysis, the effective Re values determining the composition of flow type, and thus of related shear stress, would fluctuate from zero up to their maximum values (up to 3-fold for non-supplemented, and up to 5-fold on average for albumin supplemented medium). The impact on induced stress is likely further accentuated by the stochastic nature of turbulence in general).
Table 1: Reynolds Number values for bead wake and annulus flow in Additive Solution 3 media non-supplemented (AS3) and supplemented (AS3-BSA) with 4 g/dL bovine serum albumin. View Table 1
Although change in length for beads of a given diameter resulted in coordinated increase and decline of Re associated with wake and annulus flows, change in diameter at a given length gave rise to divergent Re changes (Table 1). Oscillations of larger diameter beads were associated with wake flows having smaller Re values, and with larger Re values for annulus flows.
For flow in the bead wake, Reynold numbers' values would suggest a predominantly turbulent vortex street similar to that suggested previously for spherical beads [7]. The annular flow, however, would also depend on bead and tube dimensions, oscillation frequency and force, and sample media/environment. Notably, for the annulus, the geometry with flow-confining walls, which stiffens the flow, could be expected to increase the threshold Re value for laminar-to-turbulent flow transition. Thus, while for certain bead dimensions (at least for the overall stressing configuration/parameters used here) turbulent flows would be expected, for other bead dimensions turbulent conditions become less favorable, with a substantial part of the flow over time likely occurring in or close to a laminar fashion. Such effect could be further accentuated in albumin-supplemented media.
Although the current work is experimentally based, with inferences being drawn largely from such results, some of the interpretations naturally draw upon fluid dynamics principles. Models based on Reynolds stress evaluation had been extensively used to characterize turbulence and associated blood damage (e.g. [25,31,32]). However, such models do not account for actual turbulence structure and cell microenvironment, and thus cannot fully characterize the stresses that would impact any particular red cell. It had been shown that at least in some cases, predictions based purely upon Reynolds based stresses are inadequate in accounting for actual blood damage in turbulent flows (e.g. [28,33]). Similarly, models based upon evaluation of turbulent eddy length scales also had been shown to be a poor predictor of flow-induced RBC damage [34]. Such reports showcase the difficulties in predicting flow-induced hemolysis, for which analysis (as mentioned above) can be further complicated by cell interaction with (for example) blood proteins and biological or artificial surfaces.
Other limitations include the specific bead milling configuration employed here for MF testing, which although providing multiple variable testing parameters, may not reflect all conceivable physiologically relevant stressing variations. Further study with additional alternative bead/tube geometries and combinations, among other differences such as in the oscillation characteristics, could help to further elucidate the effects and interplay of the induced flows and stresses involved, as well as offer other opportunities to investigate potential clinical correlations. That, in turn, could better inform testing configurations, settings, and/or protocols.
RBC MF profiling can present a useful tool in exploring various aspects of RBC health or membrane damage, and this is particularly true when the testing allows varying stress types and magnitudes applied to the cells. Different causes of induced hemolysis, and of sub-hemolytic damage, vary considerably (e.g., due to blood storage, effects of drugs, extracorporeal processing, non-biological surfaces, mechanical impact of artificial valves or ventricular assist devices) and would likely be associated with different types of damage to cell membrane structures. Thus, optimal probing of such damage in RBC samples via MF testing would likely require application of stress(es) tailored to substantially target affected membrane structures of interest for given clinical applications (upon validation for such respective applications). Use of oscillating beads of different possible sizes and shapes, particularly in a bead milling configuration having other variable testing parameters, can offer users a means to control induced stresses both qualitatively as well as quantitatively.
The authors thank Kenneth Alfano for relevant discussion and manuscript review, and gratefully acknowledge Stephen Hampel for providing technical assistance including precision machining of certain components employed in the work.
The authors have been employed with Blaze Medical Devices, and authors Tarasev and Chakraborty own equity in Blaze Medical Devices. Blaze Medical Devices is a company that has developed technology relating to bead mills and bead milling based profiling of mechanical fragility (MF) of red blood cells (RBC). The Blaze technology has since been licensed out to Functional Fluidics.