The prevalence of obstructive sleep apnea (OSA) has been growing over the last few decades, but the treatment outcome differs from person to person. Interest in patient-specific modeling has increased substantially. The availability of detailed clinical data together with efficient numerical methods has now made the fluid-structure interaction modeling feasible.
The current study uses 3-D two-way fluid-structure interaction to provide simulation results of the sleep apnea symptom in a female patient with severe sleep apnea. A unique suture-patch device is presented and used to virtually apply force to the tongue.
As simulation shows, this device effectively reduced the risk of the upper airway occlusion and opened up the upper airway at the pharynx about 92% of the original area at the peak inhale volume, which will provide a possible treatment for this patient. A parametric study has been added to study the location of the patch. This pilot study may be helpful for further operation, medical treatment plan, and improvement of the curing rate.
Computational fluid dynamics, Fluid-structure interaction, Obstructive sleep apnea, Upper airway, Suture-patch device
Obstructive sleep apnea (OSA), associated with sleepiness and reduced cognitive functioning, has now been broadly recognized as a significant public health issue with numerous potential societal consequences such as accidents, increased morbidity, and cognitive deficits impairing work efficiency [1]. Daily fatigue, high blood pressure, heart stroke, and so on, may also be related to OSA. Till now, the cause of sleep apnea remains unclear. On the one hand, the overweight tongue might cause the suffocation when the patient is sleeping. On the other hand, the neurological features are also associated with OSA [2]. For mild sleep apnea patients, doctors may help them reduce weight and maintain daily exercises. For severe patients, doctors will then prescribe them to wear medical devices such like continuous positive airway pressure (CPAP) mask or perform a tissue-removal surgery. The surgery could cause permanent damage and about one-third patients can't tolerate CPAP device [3]. Moreover, the satisfactory rate of overall treatments is still less than 50%. Medical doctors have also reported that the same surgery process might have varied results on different patients. There are many factors affect the outcome of the surgery based on each individual patient. The demand of the preoperative predictions using numerical simulation approaches for each individual OSA patient keeps increasing. Recent researches in OSA using the fluid-structure interaction (FSI) modeling have developed comprehensively and made this prediction feasible. Sun, et al. [4] have firstly used FSI for the numerical simulation of the soft palate movement and airflow in the human upper airway (UA) in the nasopharynx. Chouly, et al. [5] have used FSI in a simplified manner of the geometry of the airway at the base of the tongue. Although the geometry is highly simplified, Chouly, et al. could obtain their numerical results with computational time in the order of 10 mins. Mylavarapu, et al. [6] have created the 2-D geometry of the whole UA domain and carried out FSI analysis with different inlet and outlet pressure difference. Huang, et al. [7] have built a 3-D FSI model to explore the movement of the base of the tongue during the breathing cycle. Zhu, et al. [8] have built a 3-D FSI model to study the soft palate movement during the respiration. In the same year, Wang, et al. [9] have used FSI modeling for UA and found that airway resistances significantly decrease after the nasal surgery. Zhao, et al. [10,11] have developed a novel FSI model to perform analysis of UA occlusion and flow dynamics in OSA. However, only one 2 mm layer of tissue was used as a homogeneous solid material. Pirnar, et al. [12] have performed FSI simulation of airflow in the human UA, and they have found the frequency of the snoring. Liu, et al. [13] have developed the way to simulate the UA including all the related tissues and bones in the FSI model. In this paper, the FSI modeling and simulation has been used to study the outcome of a suture-patch device which can pull the tongue forward and prevent the UA from further collapse. The current study is unique in placing suture and patch into the tongue to exert a force on the tongue. It is a brand new way in the sleep apnea treatment.
The patient is a 61-year-old female, who has been diagnosed with severe OSA by polysomnography. She has a BMI of 36 with an AHI of 80/hr. The raw 3-D UA and soft tissue models were reconstructed from the fine-cut computed tomographic (CT) images using medical image processing Simpleware ScanIP (Synopsys, Mountain View, USA). The 3-D image was then cropped into the field of 46.8 mm × 98.1 mm × 88.2 mm. The resolution was initially 1 mm, and linear resampling interpolation reduces the resolution to 0.5 mm in all directions.
Figure 1 shows the mid-sagittal view of the CT images. The soft palate is in full contact with the back wall that the air in the nose is disconnected to the air in the mouth. It can be found that the patient is breathing mainly through her mouth without considering the further movement like swallowing, coughing, etc.
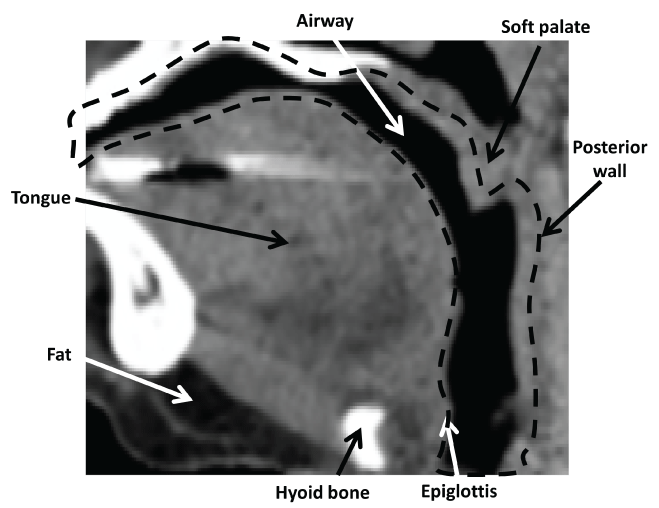 Figure 1: Mid-sagittal view of the CT image of the UA.
View Figure 1
Figure 1: Mid-sagittal view of the CT image of the UA.
View Figure 1
The geometry of the UA was segmented using ScanIP software after the 3-D CT image reconstruction. The fluid domain was reconstructed by setting the threshold value of -300 Hounsfield units, with manually smoothing the geometry and removing the islands. The bones were separated by applying the threshold value of 700 Hounsfield units. Soft tissues were then segmented manually with the anatomy knowledge and the slight different grayscale in the CT images. Figure 2 shows the mid-sagittal view of the geometry after segmentation. The black color represents the air, the ivory color represents bones, and the soft palate, the tongue, the fat under the tongue, and the walls are represented in yellow, red, blue, and green, respectively Figure 2.
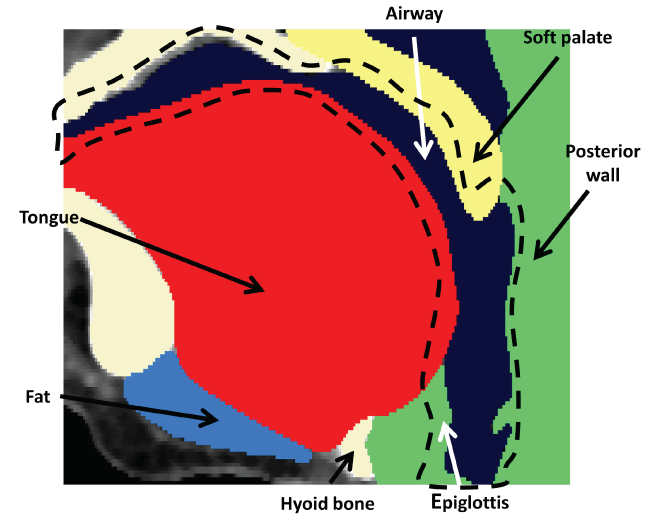 Figure 2: Mid-sagittal view of segmented geometry.
View Figure 2
Figure 2: Mid-sagittal view of segmented geometry.
View Figure 2
For the description of fluid flows the Eulerian formulation is used. The fluid problem is governed by the incompressible continuity equation and Reynolds-averaged Navier-Stokes equations (RANS) in a deformable domain ΩF, which can be expressed in tensor notation as
Where u is the velocity and P represents the pressure, ρ is the fluid density, μ is the dynamic viscosity, and t represents the time.
The k - ω turbulence model, approved to be appropriate to simulate this complex flow [6], is used as a closure for the RANS is shown below.
Where k is the turbulence kinetic energy and is specific dissipation, represents the kinetic eddy viscosity, are closure coefficients calculated by Wilcox [14], and are used for this study.
For small deformation, the structure problem under the Lagrangian framework in a reference domain Ωs is governed by the following equation, which can be derived from the Hooke's law,
Where Fi is the force, Di is the structural displacement, t is the time, and is the solid Cauchy stress tensor, which is defined as
Where E is the Young's modulus, v is the Poisson's ratio, and is the strain tensor.
The interface equations on are respectively described by the classical no-slip condition and equivalence of surface tractions as
Where and are the Cauchy stress tensor in the Newtonian fluid field and in the structural field, respectively.
The fluid part simulation was done with using ANSYS® Fluent 17.2. A pressure-based solver was used with an absolute formulation of the velocity field. The k - ω turbulence model was selected with 6% turbulence intensity and 0.02 m hydraulic diameter, which were calculated at the inlet. The SIMPLE algorithm was used to solve the pressure-velocity coupling. The spatial discretization of the pressure and momentum were both second order, the spatial discretization of the turbulence kinetic energy and the dissipation rate were both first order. Humid air was the working fluid with a constant density of 1.24 kg/m3 and a dynamic viscosity of 1.79 × 10-5 kg/m.s. The solid part simulation was done using ANSYS® transient structural 17.2. The direct sparse solver was used with numerical damping control. The Newton-Raphson residual was set as 4, and large deflection was on. The FSI system coupling was done with using ANSYS® workbench 17.2, where the interface loads from the fluid flow field were calculated and applied to the solid domain, which was solved next to extract the wall displacement to update the fluid domain. The domains were updated and solved until the two solvers reach an agreement with given relative tolerance of 1 × 10-3.
After the segmentation of the geometry, the mesh of the 3-D geometry was generated with ScanIP over the surface and the volume. The fluid model was meshed using linear four-node tetrahedral elements, and the structural model was meshed using ten-node quadratic tetrahedral elements. For different nodes densities, 16767, 29492, 58831, 181003, 190351, the pressure and velocity along a designated line (from (0.005, -0.220, -0.103) to (0.0007, -0.196, -0.138)) calculated from the simulation were compared (as shown in Figure 3). At the beginning and end of the line, it shows a difference in the pressure and velocity from different nodes densities. This is because a finer mesh can better capture the boundary layer flow physics. The pressure and velocity solved under the mesh with different nodes densities were later compared with the ones solved under a super fine mesh (with 1.2 million nodes), which the results from this fine mesh can be considered a true value. L2 norm of the errors between the results from different mesh and the true value is calculated as , where u is the variable to be compared, like pressure or velocity; and n is the number of nodes been selected. For the nodes number larger than 181003, the L2 norm of both velocity and pressure are less than 5%, so the solution can be treated as independent of the mesh size, and the nodes number 181003 is then used for the study. The non-dimensional wall distance Y+ was controlled within 5. Similar mesh study has been done for the solid structure, and it shows the nodes number 250383 is the smallest nodes number that makes the solution independent of the mesh size.
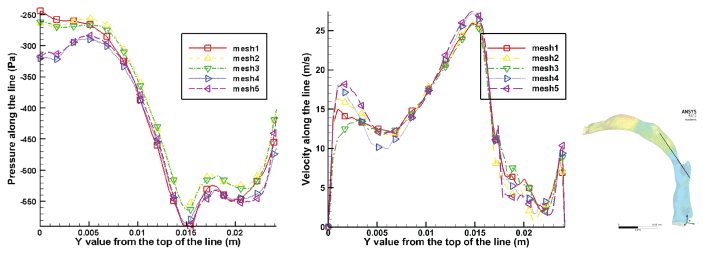 Figure 3: Mesh independent stud-pressure and velocity at different nodes densities. Mesh 1, 2, 3, 4 and 5 are corresponding to nodes number 16767, 29492, 58831, 181003, and 190351, respectively.
View Figure 3
Figure 3: Mesh independent stud-pressure and velocity at different nodes densities. Mesh 1, 2, 3, 4 and 5 are corresponding to nodes number 16767, 29492, 58831, 181003, and 190351, respectively.
View Figure 3
The air flow rate may vary from patient to patient. However, most people from clinical observation have a similar breathing flow rate curve, and Gupta, et al. [15] have studied and published it. The breathing rate described by them can be simplified to a sine curve. The peak volume flow rate is 0.4 L/s, which would result in a pressure difference of 200 Pa between the inlet and outlet. In this present study work, pressure inlet and pressure outlet were used as boundary conditions, with 0 Pa as the inlet pressure, and -200 Pa for the outlet pressure.
On the structure side, the hard palate and the spine were set to fixed support where the deformation was considered zero. The bottom surface of the geometry which connects to the lower larynx was set with no deformation in the z-direction, but it was still free to move horizontally. The contact type selection was critical in the simulation. The interface between the soft palate and the back wall or the tongue was frictionless, and the contact between the tongue and the suture was frictionless, also the contact between the tongue and the lateral wall was frictionless. The tongue was only bounded on the hyoid bone and the center of the lower half of the mandible.
The suture-patch device is intended for exertion force to the base of the tongue with a suture and a patch as shown in Figure 4. The suture goes from the epidermis to the fat under the tongue, through the digastric muscle, and goes through the tongue from the middle where there is an approximately 2 mm wide hollow in the tissue and won't cause too much uncomfortable feeling during the pulling. The patch can be pasted on the surface of the tongue, or it can be worn with a little suction force which holds it to the tongue. The purpose of using a patch is to let the force evenly apply on the tongue and reduce the possible penetration due to high normal stress. Medical doctors have suggested the diameter of the patch to be between 1 and 1.5 cm, and based on the size of the upper airway and the shape of the tongue, 13.3 mm is select as the diameter of the patch. Three different locations: above the velopharynx (patch location 1), at the velopharynx (patch location 2) and below the velopharynx (patch location 3) were selected respectively to put the patch. The suture is straight from the center of the patch to the middle point right under the lower jaw to let the device easy fix to the lower jaw. The device is going to be a battery or mechanical operated spring that screwed to the bottom of the lower jaw and controls the pulling force with multiple clicks. This paper focuses on the suture, patch, and force analysis, and the device will be discussed in the future work.
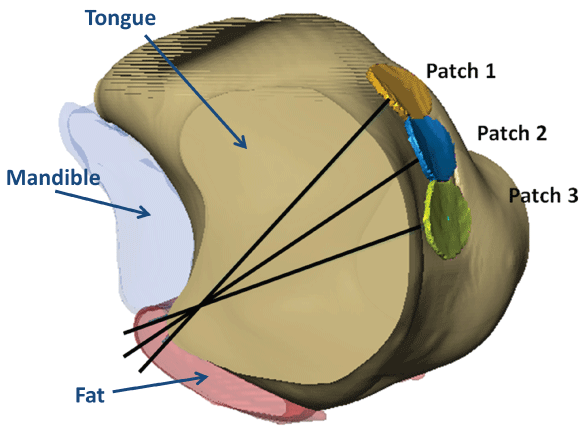 Figure 4: The suture-patch locations in the tongue.
View Figure 4
Figure 4: The suture-patch locations in the tongue.
View Figure 4
The suture has to be non-dissolvable, low plasticity, with strong thread memory (not flexible, non-braided), better with a straight needle, round point type. The suture's surface should be smooth and even, with good pliability, and the suture's diameter is optimized with a 0.8 mm diameter to prevent possible tissue cut through the tongue. Also, the suture, which is designed came out slightly under the lower jaw, is aimed to be pulled perpendicularly to the patch to reduce the shear stress along the tongue surface tissue. In the simulation, the suture is assumed to have a low enough plasticity that the suture can retain its length and strength after stretching, or say that the shape change of the suture can be recovered. It is then remaining the same force through the suture.
The patch can be shaped to fit the surface of the tongue with ScanIP, and it then can be printed from a 3-D printer. The patch is designed as a 13.3 mm diameter round shape with a thickness of 0.8 mm. The thickness was concluded with the consideration of the computational cost. But in reality, the thickness of the patch can go even lower to 0.1~0.2 mm, as long as the boundary is smooth with no sharp edge. The stiffness of the patch should also be considered. On the one hand, the patch should be light and soft; when people swallow or talk, it should be fixed and moved with the tongue without causing uncomfortable foreign matter feeling for the patient. On the other hand, it is there to help the suture exert the force evenly on the base of the tongue, so it should be firm, leading the shape change of the tongue. The material of the plate is very critical, after careful consideration, titanium is chosen in the present study, as it is widely used in the medical area due to its biocompatibility.
The linear elasticity of different tissues used in the current study is based on the published papers and our porcine experiments [16], which are shown in the Table 1 below.
Table 1: Young's modulus and Poisson's ratio for the tissues. View Table 1
As mentioned in the previous section, the FSI system coupling simulation was performed to study the fluid and solid interaction. On the fluid side, the pressure difference between the inlet and outlet has ramped up till 200 Pa, and the velocity field is coupled with the pressure field by the SIMPLE algorithm. Figure 5 shows the velocity streamlines without and with 5 N force on the suture. The color represents the magnitude of the velocity with the same legend. It can be found that without force the UA is collapsed at the oropharynx, where the red color shows a maximum velocity of 22.0 m/s. Shortly after going inside from the inlet of the mouth, a small recirculation occurs because of the reduced fluid flow area where the hard palate is close to the middle of the tongue. A stronger recirculation occurs at the cavity between the tip of the soft palate and the back wall. The disturbance around the epiglottis is less than those mentioned by the previous literature [13] since the epiglottis here is fully contacted with the inferior wall and results in no bifurcation. This could be a patient-specific phenomenon. After the force added along the suture, the airway is opened up not only in the velopharynx area, but also in the part that under the hard palate. The flow is slower and smoother after the force has been applied to the suture-patch device.
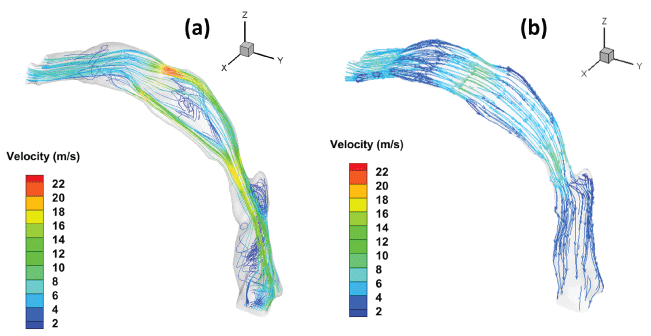 Figure 5: Velocity streamlines of the UA (a) Without and (b) With 5 N force along the suture.
View Figure 5
Figure 5: Velocity streamlines of the UA (a) Without and (b) With 5 N force along the suture.
View Figure 5
The cross sections were taken at eight different transverse planes, whose distance from the outlet are 66 mm, 62 mm, 58 mm, 54 mm, 50 mm, 46 mm, 42 mm, and 38 mm in turns as shown in Figure 6. The collapse happened at the fourth plane where the right side of the soft palate has touched the tongue. The outline of cross-sectional plane shows this change. At that moment, the volume flow rate is 0.39 L/s, and the average velocity at the throat is 22.0 m/s. After the soft palate touching the base of the tongue, the reduced area will cause stronger pressure to drop at the pharynx, which will expedite the collapse procedure.
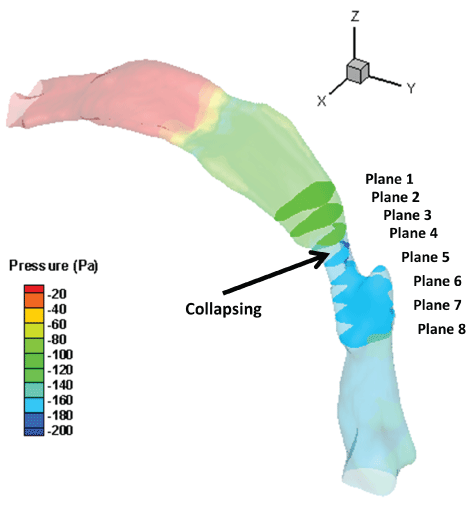 Figure 6: Cross-sectional planes showing the location of collapse.
View Figure 6
Figure 6: Cross-sectional planes showing the location of collapse.
View Figure 6
With the same pulling force of 5 N, the cross-sectional areas of the eight planes are calculated and compared as shown in Figure 7. Without considering the device that connected the suture to the bone, the Patches 2 and 3 each can open up the plane 4 about 92% of its original area and gives a wider space for the air to flow through. This also will reduce the possible snoring which results from the soft palate hitting the base of the tongue. Patch 1 performs better in the upper area but not perform well in the collapsing region. Patch 3 is the closest to the vertical direction, which is pulled nearly horizontally, this works well when the patient is laid down. Patch 1 and 2 have a larger angle with the vertical direction, which means only partial of the force work on the airway opening. However, Patch 3's vertical position might result in uncomfortable feeling since it is close to the epiglottis, so it is not suggested. Patch 2 has a similar effect at the collapsing region, and the location is upper than Patch 3. Based on this pilot study about this specific patient, Patch location 2 is suggested which will open up the airway about 92% of its original area, which located right in front of the tip of the soft palate.
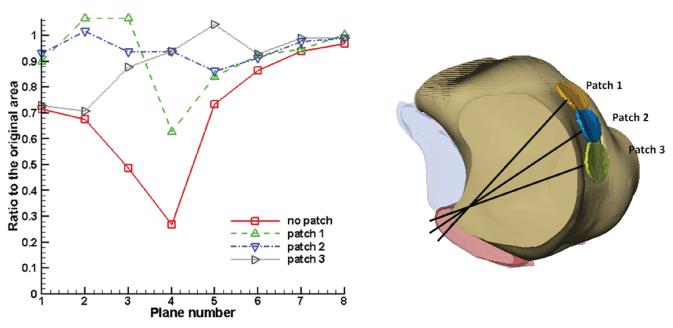 Figure 7: Area change due to the locations of the patch.
View Figure 7
Figure 7: Area change due to the locations of the patch.
View Figure 7
Deformation contours of the inhaling with 5 N forces applied along the suture at three locations are shown in Figure 8. It can be found that with the applied force, the UA is opening up from collapsing. The soft palate is never touching the tongue on the front side. In point of fact, on each side of the tongue, there is one palatoglossal muscle connected to the soft palate that will draw the soft palate forward. However, for simplification, the muscles and their functions have not been considered in the simulation. Therefore the soft palate did not move forward much in the simulation. However, as the soft palate is dragged forward by the palatoglossal muscle, the airway that from nose might be opened up from the closed status at the CT scanning. It is noticed that the three patches are not along the same vertical line since the respiratory tract is not symmetrical.
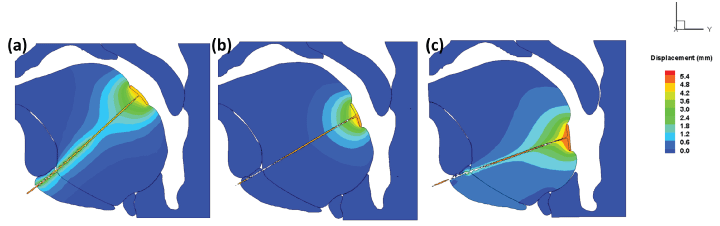 Figure 8: The deformation contours with 5 N forces along the suture for (a) Patch location 1, (b) Patch location 2, (c) Patch location 3.
View Figure 8
Figure 8: The deformation contours with 5 N forces along the suture for (a) Patch location 1, (b) Patch location 2, (c) Patch location 3.
View Figure 8
Figure 9 shows the von-Mises stress generated in the suture, patch and the tissues in exponential legend. As expected, important variations in terms of stress amplitudes are observed in the suture and across the tissues. In the stress is up to 20 MPa, which results from the 5 N force on the small contact area. The stress on the tongue tissue is not that high, which is because the frictionless contact between the tongue tissue and the suture and results the stress is highly affected by the area of the patch which largely reduced the normal stress came from the 5 N force. In the former published work, the maximum active stress values in the tongue muscles are below 150 kPa [9], which the stress in the suture is larger than that. The stress in the suture has risen up to tens of MPa, but in the tongue tissue, it is within 5 kPa. The aim of using the patch is to reduce the equivalent stress in the tongue. There should be no harm to the patient's speaking abilities since the force on the suture can be controlled to work only during sleeping time. The discomfort from the patch should be similar to those have a tongue piercing bead. The patient should be able to use the tongue as usual when she's awake.
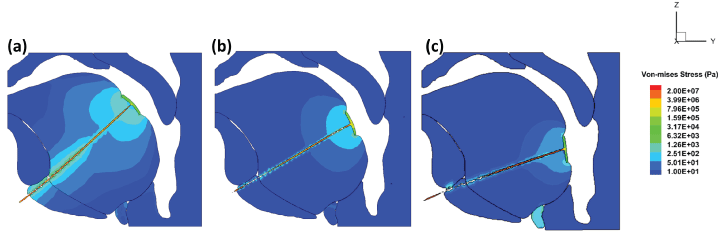 Figure 9: The von-Mises stress on the suture and in the tissue with 5 N force along the suture for (a) Patch location 1; (b) Patch location 2; c) Patch location 3.
View Figure 9
Figure 9: The von-Mises stress on the suture and in the tissue with 5 N force along the suture for (a) Patch location 1; (b) Patch location 2; c) Patch location 3.
View Figure 9
In the previous section, a guessed value of 5 N is used as the pulling force based on previous clinical experiments on volunteer patients. Then, the bisection method is used to find the minimum force needed to open up the upper airway. The bisection method is a root-finding method that repeats bisects an interval and then selects a subinterval in which a root must lie for further processing. In this case, it is used to bisect the interval of effective and ineffective force to open up the UA, until the minimum force is found.
Figure 10 shows the results of the cross-sectional area at selected planes when using different pulling forces. It can be seen that the area varies most in the plane 3 and 4 that is the center of the patch located. The UA will collapse when there is no force. While breathing in, 0.94 N force is able to pull the tongue and open up the cross-sectional area to its original size. While 0.63 N is not enough. And F = 1.25 N is able to pull the UA cross-section area larger than its original value which should be suggested. 2.5 N and 5 N can open up the airway more than needed, which may cause uselessly uncomfortable for the patient. So it is suggested 1.25 N can be used as the initial pulling force for this specific patient. And the force will be able to be adjusted above or below this value based on the patient's actual feeling.
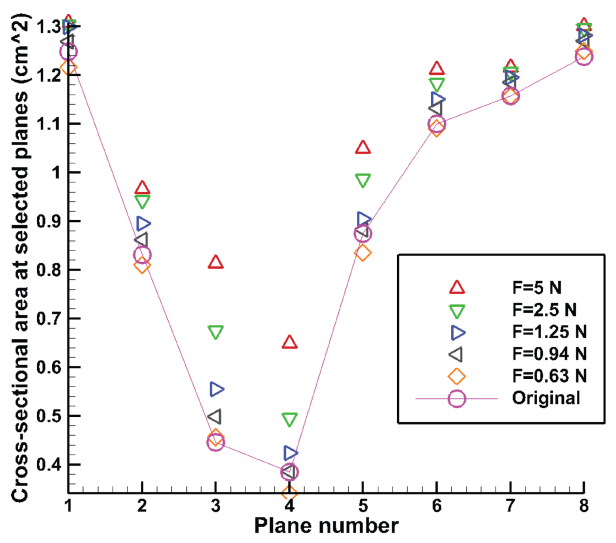 Figure 10: Cross-sectional area at selected planes with different pulling forces.
View Figure 10
Figure 10: Cross-sectional area at selected planes with different pulling forces.
View Figure 10
In this paper, a pilot study of the suture-patch device to relieve the sleep apnea symptom was established and analyzed. The patch can be 3-D printed to better match the person's tongue shape, and the suture can be easily acquired from the hospital. The applied force can be controlled with advice screwed on the lower jaw, which will be designed in the future work. The results show that the suture patch device can open up the UA for this specific patient. This overbears the most irreversible surgical procedures that might cause substantial patient morbidity. Also, the cost can be controlled and the surgery is not difficult to perform. Though it is a pilot study, the result shows that it has great potential to help severe sleep apnea patient to open up the UA. Three patch-suture positions are studied, and the best of them can open up the UA about 92% of its original area. The von-Mises stress on the surface of the tongue was simulated and it is far from causing any tearing or damage. Bisection method was used to find the minimum force needed to open up the UA while inhaling, which will further reduce the uncomfortable feeling. In the future work, more patients will be involved in the study and some experimental study may be carried out after more simulation results are achieved.