The primary focus of the nanotechnology therapeutic approaches has been on early disease detection, drug discovery and monitoring, controlled release of therapeutic agents, and targeted drug delivery. Targeted drug delivery system requires more research including statistical modeling to establish the reliability in success of drug targeting. This part of every nanotechnology therapeutic approach is especially fundamental for reaching stronger therapeutic effects with lower side effects.
In practice, we may be unable to accurately assess our nanotechnology drug delivery system designs to improve the reliability. This is likely due to the lack of a unified definition of reliability in system design phase. For this shortcoming, we introduce the notion of reliability in this context. Our proposed notion of reliability is flexible in allowing a general method for determining dose level. We then describe a methodology that enables us to determine an optimal dose level to achieve certain reliability. Although, in this report we focus on a special nanotechnology drug delivery system for cancer therapy, i.e. folate-conjugated gold nanoparticles for transfer to over expressed-folate-receptor cancerous cells, our developed strategies can be applied to many other drug delivery systems as well.
Poisson distribution; Binomial distribution; Nanoconjugate; Folate receptor.
| c | the number of nanoconjugates that are carrying the drug and they are injected into the blood stream |
| P* | the probability that any of C nanoconjugates be able to penetrate the tissue |
| λ1 | the average number of folate receptors for a healthy cell in the tissue |
| λ2 | the average number of folate receptors for a cancerous cell in the tissue |
| λ | the average number of cells in the tissue |
| P | the chance of a cell being a cancerous cell in the tissue |
| the chance of a nanocojugate that is carrying the drug to penetrate a cancerous cell in the tissue | |
| k | the number of nanocojugates, carrying the drug, needed to destroy a cancerous cell in the tissue |
| Φ | the cumulative distribution function of the standard normal distribution |
| zα | the α percentile of the standard normal distribution. |
It goes without saying that advances in life- and physical-sciences and engineering have contributed greatly to the improvements made in our quality of life and wellbeing. Molecular-based study of processes is the basis of modern life and physical-sciences and engineering. In the 20th century, technological approaches to solve problems of healthcare, quality of life and human communications started its alteration from a merely rational science to a scientific technology with fully atomic and molecular basis. At first, antibiotics which meddled with pathogens at the molecular level were engineered and introduced. Then, the ongoing developments in chemical and statistical physics, genomics, and now nanobiotechnology have been providing ever more precise knowledge of the functions of the different micro and macro organism, and mechanisms underlying living things, infections and diseases at the atomic and molecular level. In other words, understanding of life advanced from understanding the functions of organs and tissues to the functions of cells and finally nano scale systems as well as supra-, macro- and individual-molecules [1-8].
Nanotechnology developments were initiated during the last decade of the 20th century when we had already achieved profound molecular awareness about the living systems in general and human body in particular. Generally, nanotechnology is the science of dealing with molecular scale systems and matters. Such systems and matters being worked on through nanotechnology have the following three important features [2].
(a) They have at least one of their three dimensions in between 1 to 200 nm.
(b) There are some techniques with control on the physical and chemical characteristics of structures in molecular scale.
(c) They are able to be assembled together to generate larger structures.
These features are applicable to all natural and microbiological systems including bio-systems such as cells, bacteria, enzymes and viruses.
The simultaneity between the launch of nanotechnology development and our molecular awareness of living systems has resulted in introducing a molecular-based technological medicine in which the molecular basis of life is manipulated to construct specific desired results through nanotechnology methods and devices. In other words, the knowledge of human molecular structure is used to design biomedically active microscopic devices in the 21st century. These devices will be used for missions of cellular inspection, repair, and reconstruction. Therefore, the 21st century treatment through nanobiotechnology is expected to entail the proliferation of efficacious therapeutic molecular tools to establish and maintain a continuous state-of-health for humans [1,3].
Accumulating evidence suggests that lack of balance between proliferation and apoptosis may cause cancer emergence [4]. Suppression of apoptosis hinders many forms of cancer therapeutic strategies, including radiation therapy, cancer immunotherapy and chemotherapy [5]. Elimination of cancer cells by early apoptosis is preferred over other forms of cell growth inhibition. Apoptosis directly leads to tumor regression and reduces risks of selecting more aggressive and/or drug resistant phenotypes (any observed quality of an organism) that are often responsible for tumor re-growth and treatment failure [6]. Apoptosis also plays a critical role in the cytotoxic activity of a wide range of anticancer agents, including chemotherapeutic agents, biological agents and hormones. Defects in apoptosis pathways are associated with drug resistance in many cancers [7].
Generally, the focus of the nanotechnology therapeutic approaches to treat cancer has been on early disease detection, drug discovery and monitoring, controlled release of therapeutic agents, and targeted drug delivery. Targeted drug delivery requires more research and it is especially fundamental for reaching stronger therapeutic effects with lower side effects. This part of every nanotechnology therapeutic approach requires statistical modeling to establish the reliability in success of drug targeting. In this paper we first introduce the notion of reliability for a nanotechnology drug delivery system. We then report on our efforts to determine an optimal dose of the drug to achieve a particular reliability for a cancer nanotechnology drug delivery system.
This paper is organized as follows. In Section 2 for a specific number of nanoconjugates that are carrying the drug and they are injected into the blood stream, we present a dynamic model for the number of nanoconjugates that penetrated cancerous cells population in the tissue. Similar to our proposed model was used by [8] to model the number of nanoconjugates that might attach to surface of a cell. In section 3, we introduce the notion of reliability and give algorithm to compute an optimum dose level to achieve certain reliability. Several examples are given in this section to illustrate our proposed methodology. Concluding remarks are provided in Section 4.
Let us consider a nanoconjugate containing the drug, (for example folic acid connected to a cancerous cell killing agent or gold nanoparticle which the hypothermia agent, or drug, through a linker, like a thiol molecule (Figure 1)), which has potential to enter a cancerous cell in a tissue that has on its surface over-expressed folate receptors [9,10].
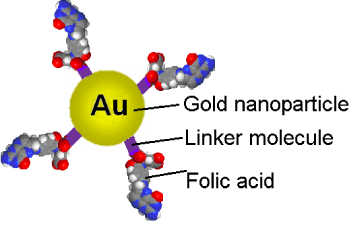 Figure 1: Nanoconjugate formed by folic acids or folates, attached to gold nanoparticles through a linker like a thiol molecule [[9]]. View Figure 1
Figure 1: Nanoconjugate formed by folic acids or folates, attached to gold nanoparticles through a linker like a thiol molecule [[9]]. View Figure 1
Suppose c is the number of these nanoconjugates that are injected into the blood stream. Now, out of c nanoconjugates, let L be a discrete random variable representing the number of nanoconjugates that permeate a tissue. Then, L has Binomial distribution with the probability distribution function.
Where p* is the probability of any nanoconjugte carrying the drug being able to penetrate the tissue. From the equation (2.1), the average number of nanoconjugates that reach the tissue is cp* [11]. It is worth mentioning that in practice, p* is usually a function of velocity of a blood flow. Velocity is a function of (x,y,z), but when it gets to cell it really does not matter if it has vectorial character, but for the macroscopic system it is a vector.
Let X and Y be the number of folate receptors for healthy and cancerous cells, respectively. Since cancerous cells are normally bigger than normal cells, i.e., a cancerous cell has more folate receptors than an healthy cell, so that X is stochastically smaller than Y [12]. To study stochastic behaviors of both random quantities, we assume that X and Y have Poisson distributions with parameters λ1 and λ2, respectively. Here, the parameter λ1 is the average number of folate receptors for a healthy cell and the parameter λ2 is the average number of folate receptors for a cancerous cell and λ1 ≤ λ2. For more details about Poisson distribution see [11]. In reality, cancerous cells and healthy cells are not well distributed in the tissue. That is, the number of healthy cells and cancerous cells are both dynamic. Thus, stochastic models needed to model the number of cancerous cells as well as healthy cells in the tissue. For that, we let the total number of cells in the tissue be represented by Z, where Z has Poisson distribution with the parameter λ. The parameter λ is the average number of cells in the tissue. Suppose the chance of a cell being a cancerous cell is p and the chance of being an healthy cell is 1-p. Then, Z1, the size of cancerous cells population in the tissue, is Poisson with parameter λp and Z2, the size of healthy cells population in the tissue, is Poisson with the parameter λ (1 - p). The parameters λp and λ (1 - p). represent average numbers of cancerous cells and healthy cells in the tissue, respectively.
Define a binary random variable W such that W=1 if a nanoconjugate which is already inside the tissue enters a cancerous cell and W=0 if it enters a healthy cell. Then, P(W=1) is approximately equal to (Appendix 1). Since a cancer nanotechnoloy drug delivery system is applicable when λ1 is much smaller than λ2, i.e., λ1 < < λ2, therefore the chance of a nanoconjugate penetrates a cancerous cell is much higher than an healthy cell. Suppose L1 represents the number of nanoconjugates that reach the cancerous cells population in the tissue, then one can proof that L1 has Binomial distribution with parameters c and . That is, the average number of nanoconjugates that reach the cancerous cells population in the tissue is (Appendix 2). It should be noted that this number is expected to be much higher than the average number of nanoconjugates, that reach healthy cells population in the tissue.
Since the particular mechanism can make a big difference in the number of nanoconjugates delivered to the cancerous cells and since different modes of photo dynamic therapy require a different number of nanoconjugates needed to kill a cancerous cell, we assume that one needs k nanoconjugates to penetrate a cancerous cell and kill it [13,14]. Here k is provided by an expert. Now, the chance of a cancerous cells population having size 1, Z1=1, being killed for given c is
Table 1 gives values of B (k,c) for different values of k and c when λ2=10, λ1=1 and p*=0.9. Binomial Table can be used for other values of parameters.
For example from Table 1, given that we need k=3 nanoconjugates to kill a cancerous cell, six nanoconjugates, c=6 will kill the cancerous cell with probability 0.988. That is, six nanoconjugates should be injected. As discussed [14], in some situations the size of a nanoconjugate is much smaller than the size of a cancerous cell and therefore one needs to deliver hundreds of nanoconjugates to kill a cancerous cell. So in (2.2) if we take c=500, then we need to inject c=743 nanoconjugates to make sure that the cancerous cell will be destroyed with probability 0.988. Again we emphasize here that it is assumed the tissue has only one cancerous cell and about 82% of injected nanoconjugates penetrated the cancerous cell.
Table 1: Values of B(K,C) for given values of C and k. View Table 1
Let N be the number of cancerous cells in the tissue that will be killed with C injected nanoconjugates. Then we call a nanotechnology drug delivery system to be 100a percent reliable if P (N=Z1) =α. Statistically speaking, the system's reliability is a if we are 100α% confident that all cancerous cells in the tissue will be destroyed by this nanotechnology drug delivery system. It is worth mentioning that our definition of a reliability is different from the classical definition of reliability where a system's reliability is defined in-terms of its lifetime [15]. Our proposed criteria to find an optimal c is: Find the smallest c that achieves 100α% Reliability.
Using our criteria, c must satisfy the following equation.
Now in the equation (3.1), we need to calculate P(N=z|Z1=z) Using the equation (2.2), it is clear that P (N=0|Z1=0)=1 and P(N=1|Z1=1) = B (k, c). Given that a cancerous cell is killed, suppose the chance that it was killed by j nanoconjugatesis, aj where j=k, k +1,…, that is, P (a cancerous cell was killed by j nanoconjugates|a cancerous cell was killed) =aj. Throughout this paper we assume that ak=1. That is, given a cancerous cell is killed, the chance that it was killed by k nanoconjugates is 100%. Since c is usually large, using Poisson approximation for Binomial distribution, we can assume that L1, the number of nanoconjugates that reach cancerous cells population in the tissue, is Poisson with the mean
In the equation (3.3), Φ stands for the cumulative distribution function of the standard normal distribution function [12].
In the appendix 3, we provide R-codes to calculate the middle part of the equation (3.1) using the equation (3.3) [16]. Applying this program, one can calculate the reliability of a nanotechnology drug delivery system. The following example illustrates that.
Example 1: Suppose we have designed a nanotechnology drug delivery system with c=420, k=3, λ=1000, p=0.1, λ2=20, λ1=1 and p*=0.95. Using the R-program we get P (N=Z1)=0.98 at is, this system is 98% reliable. However, if we move from p=0.1 to p=0.9, then the system is 0% reliable. That is this drug delivery system is highly unreliable.
Now to obtain our optimal c that achieves 100a% confidence, we propose the following algorithm.
(a): Choose an initial value for c say c=c0, then compute P (N=Z1) using our R-program. If this probability is less than a, take c=c0 + 1 and compute the probability again. Continue this until for the first time the probability is greater than or equal toa.
(b): If for c0, the probability is more than a. Then, take c=c0 – 1 and compute the probability again. Continue this until for the first time the probability is less than or equal to a. Suppose c* is the answer. Now, if for c=c*, the probability is exactly a, then the optimal solution is c*. If it is less than a, then the optimal solution is c=c* + 1
Several comments are in order with regard to our proposed Algorithm.
(1) To implement the algorithm, we need to provide k, λ, p, λ2, λ1 and p*.
(2) Our recommendation is as an initial value for c take c0=(k λp) + (Za k(λp)0.5), where Za is a percentile of the standard normal distribution.
(3) To calculate probabilities for Binomial and Poisson distributions sometimes one needs to use Normal approximations for both distributions [11]. The following example illustrates implementation of our Algorithm.
Example 2: In this example, we describe four different scenarios.
(a) Let k=3, λ=1000, p=0.1, λ2=20, λ1=1 and p*=0.95. Suppose our goal is to design a nanotechnology drug delivery system that achieves 95% reliability. To find C that guarantees such reliability, as mentioned in (2), we start with c0=360. Using our R-program, for this number the reliability is 75.5%. So to increase the reliability, we move to c0=361. Still for c0=361 the reliability is lower than 95%. So we continue until we reach the threshold 95%. For this nanotechnology drug delivery system, the optimal solution is c = 400. That is, one needs at least 400 nanoconjugates to inject into the blood stream to achieve the reliability of 95%.
(b) In the part (a), take c = 0.90 and keep the values of other parameters the same. That is, we assume that 90% of cells in the tissue are cancerous cells. Applying our Algorithm, we start with c0=2880 for, 2880 nanoconjugates the reliability is 15% which is much lower than 95%. We continue increasing number of nanoconjugates until we get 95%. The optimal solution is c=3191. That is, we need 3191 nanoconjugates to inject into blood stream to achieve the reliability of 95%.
(c) In the part (a), take p=0.90 and k=1and keep the values of other parameters the same. That is, assume that 90% of cells in the tissue are cancerous cells and to kill a cancerous cell one nanoconjugate is required. Applying our algorithm, we start with c0=960. For, 960 nanoconjugates the reliability is 20% which is smaller than 95%. We increase the number of nanoconjugates in order to achieve our goal of 95% reliability. The optimal answer is 1080. It is interesting to note that by moving from k=3, part (b), to k=1, the dose level (the number of nanoconjugates) needed to achieve the same reliability is much less.
(d) In the part (a), take p=0.9, and keep the values of other parameters the same. If we want our system to be 99 % reliable, we need 4028 nanoconjugates.
In this paper, we have introduced a unified definition of reliability for a nanotechnology drug delivery system. This notion provides a general framework for carrying out determination of unknown dose level in order to achieve a specific reliability for a nanotechnology drug delivery system. Our proposed method is very flexible and easy to use. As one expects our finding shows that, one can achieve a specific reliability with low dose level by having small k, the number of nanoconjugates needed to kill a cancerous cell. By increasing k, the dose level increases exponentially. Also, by increasing the reliability level, the dose level increases.
The work of the first author is partially supported by the National Science Foundation, DMS1208273. We would like to thank the reviewer for very constructive comments that lead to improvement of the paper.