International Journal of Sports and Exercise Medicine
High-Resolution Accelerometry Resolved by Time-Frequency and Principle Pattern Analysis
W Jeffrey Armstrong1*, John D Welch2, Frank Borg3 and Travis W Beck4
1Division of Health and Exercise Science, Western Oregon University, USA
2College of Public Health and Human Sciences, Oregon State University, USA
3University of Jyväskylä, Kokkola, University Consortium Chydenius, Finland
4Department of Health and Exercise Science, University of Oklahoma, USA
*Corresponding author: W Jeffrey Armstrong, Division of Health and Exercise Science, Western Oregon University, 345 N. Monmouth Avenue, Monmouth, OR 97361, USA, Tel: 1-503-838-8999, E-mail: armstoj@wou.edu
Int J Sports Exerc Med, IJSEM-1-012, (Volume 1, Issue 3), Research Article; ISSN: 2469-5718
Received: March 18, 2015 | Accepted: June 23, 2015 | Published: July 03, 2015
Citation: Armstrong WJ, Welch JD, Borg F, Beck TW (2015) High-Resolution Accelerometry Resolved by Time-Frequency and Principle Pattern Analysis. Int J Sports Exerc Med 1:012. 10.23937/2469-5718/1510012
Copyright: © 2015 Armstrong WJ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The measurement peak-to-peak amplitude high-resolution accelerometery (HRA) during single-leg balance has been shown to be reliable. In the present (repeated measures design) study, the HRA signal was transformed into a wavelet-based HRA-intensity-pattern and analyzed using principle components analysis. Subjects (5M/5F, 25 ± 3 yr; 169.4 ± 11.7cm; 79.0 ± 16.9kg) participated in fifteen (3 randomized bouts of 5 repetitions) 15-s dominant-leg stances. A single HRA was fixed superficial to L3/L4 segment to capture motions relative to the center-of-mass and streamed to a base station (sample rate=625Hz). Signals were sampled, recorded and later analyzed. HRAs were recorded in g's for vertical (VT), medial/lateral (ML), anterior/posterior (AP), and resultant (Res; ) directions. To test the repeatability of the data, repeated measures ANOVA were performed on the k (i.e., 3) principle patterns (i.e., p-vectors) for each direction for the 15 trials on the principle patterns of the average HRA-intensity-pattern (of the 5 trials) for each session. These were followed with the calculation of the intraclass correlation coefficients (ICC), standard error of the measurement (SEM), and the repeatability coefficient (CR). For the repeated measures ANOVA of the p-vectors, the only significant differences were observed for the within Session effects for P-1 and P-2 in the AP direction (p=0.042 and 0.022, respectively), within Trials for P-2 in the AP direction (p=0.042), and within Sessions for P-1 for the Res direction (p=0.027). ICCs were ± 0.07, with the exception of the vertical direction (ICC ± 0.961); SEM ranged from ± 0.073 to ± 0.322; and CRs from ± 0.202 to ± 0.891, thus demonstrating poor repeatability. These data demonstrate that the HRA-intensity-pattern can reveal subtle variations in posture control strategy, however, may not be a reliable instrument for comparing measurements of dynamic balance without the context of other tools.
Keywords
Accelerometer, Intensity-pattern, Posture control, Quiet stance, Single-leg
Introduction
According to Blaszczyk et al. [1], the ranges of the postural limits define the perimeters of stability and represent the extent to which the COM travel before one loses balance. Uushiyama and Masani [2] suggest that the maintenance of the body's center of mass (COM) within the base of support defines postural stability. Thus, postural stability is the result of the many forces acting on the body to retain the COM within the base of support and can be approximated by recording trunk accelerometry via a high-resolution accelerometer (HRA) placed at the intersection of the sagittal and axial planes on the posterior trunk in line with the posterior superior iliac crests (superficial to L3/L4) [3]. If one considers that the erect body moves as an inverted pendulum COM accelerations/velocities would reflect increased postural sway. This is supported by Moe-Nilssen and Helbostad [4] and has been demonstrated to be reliable [3,5].
HRA can be used to either stream data at high frequency in real time, or data-log signals collected during a variety of "real world" activities. Through recent technological advances, microelectromechanical system accelerometers (MEMS) are increasingly available and affordable devices that make HRA a viable and useful tool in balance and gait studies [3-8].
In a previous study, Armstrong and coworkers [9] examined the effects of fatigue on single-legged postural stability using mechanomyography (MMG) and HRA. Specifically, the researchers evaluated the reliability of a protocol for using a MEMS-HRA to measure COM accelerations in the three cardinal planes and uniaxial accelerometers (ACC) to measure MMG in key postural muscles of the lower extremity and the relationships between HRA and ACC during single-leg balance. The researchers concluded that the peak-to-peak amplitude measurements of these bioelectrical signals provide reliable information pertaining to the control of postural stability [9].
The bioelectrical signals recorded using HRA and MMG, as well as surface electromyography (sEMG), are, however, complex and nonstationary. This presents a challenge in capturing the totality of what is occurring with these signals over time. The common practice of averaging the root mean squares potentially misses subtle changes that occur to the signal (e.g., frequency changes) over time. Thus, a variety of approaches have been tried to provide greater information regarding the signal over time. McGregor and others [6,10-12] have examined the complexity of the MMG and HRA using control entropy. Others have examined the use of principle component analyses in the examination of the complexities of kinematic and electromyographic data (e.g., see Daffertshoffer et al. [13] and von Tscharner et al. [14]).
A useful tool in analyzing bioelectrical signals in the time-frequency domain is the "intensity analysis", developed von Tscharner [15] for sEMG, adapted by Beck et al. [16] and Armstrong et al. [17] for MMG, and by Armstrong et al. [18] for HRA. The intensity analysis uses a filter bank of nonlinearly scaled Cauchy wavelets that are optimally spaced in the frequency domain to approximate the power or "intensity" of the nonstationary signal in time [13,14]. von Tscharner [15] equated intensity to the traditional idea of power in frequency space (i.e., the power spectrum) and a function of both time and frequency. Thus, while the intensity analysis is developed specifically for the analysis of no stationary sEMG signals [15] and, subsequently, for MMG [16,17], it is possible to use the tool to describe the nonstationary events (e.g., onsets, durations, oscillations, and frequency distributions of electrical signals) in other physiological signals (e.g., the oscillations of the body's COM during quiet stance or gait. Recently, Armstrong et al. [18] published the application of the intensity analysis to HRA (HRA-intensity-analysis).
A challenge remains in the statistical analysis of data from the intensity analysis. Because the output creates a sort of "cloud" of three-dimensional data (i.e., time x frequency x intensity amplitude; see figure 1), analysis of inter-trial samples is difficult using traditional statistics (e.g., repeated measures ANOVA). Thus, one is left with comparisons of the data compressed into two-dimensions (e.g., total intensity or the frequency spectrum [15-18].
.
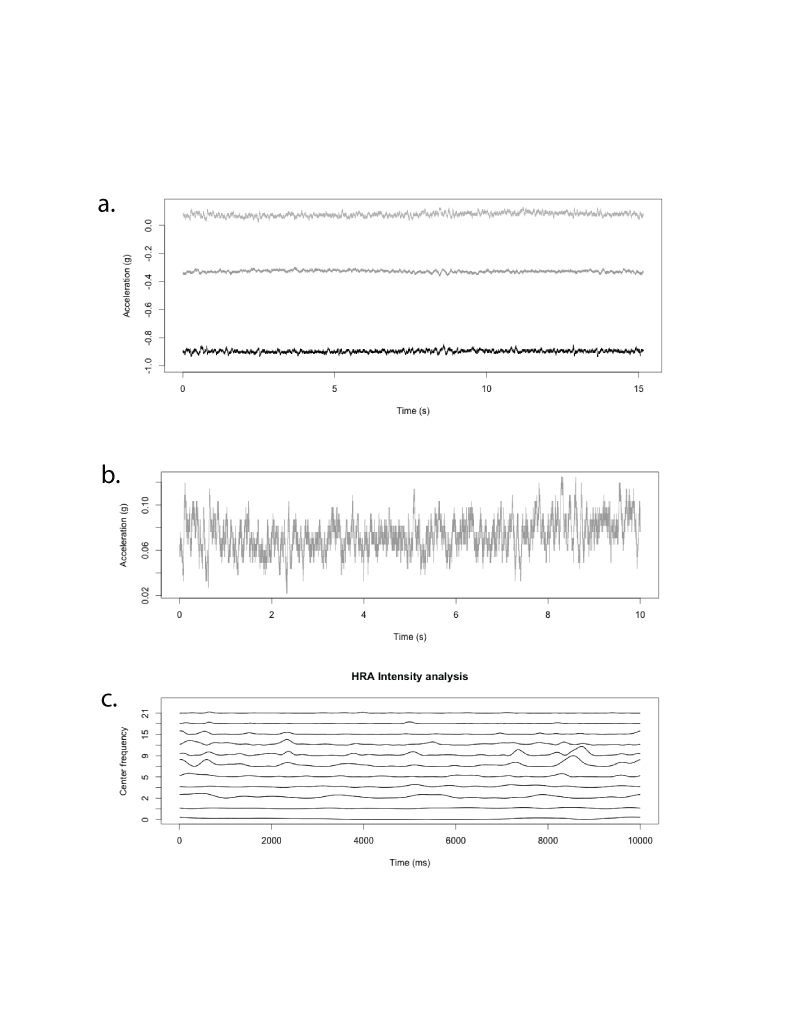
Figure 1: (a.) Sample raw HRA data for the VT (black line), ML (gray, top line), and AP (dark gray, middle line) (subject 1; PreRest, trial 5); (c) intensity analysis of a 10-s segment (b) of HRA data for VT of the sample data.
View Figure 1
To address these challenges, von Tscharner [19] has applied principle component analyses (PCA) using what he has termed pattern space or "p-space" [19,20]. Similarly, Castells et al. [21] apply PCA to electrocardiography. Daffertshoffer and colleagues [13] present a tutorial on the application of kinematic data and EMG. Thusly, p-space may be used to discriminate between other nonstationary, bioelectric signals such as HRA that have been subject to the intensity analysis.
The purposes of the present analyses were to i) detail and apply the steps to define p-space for the analysis of HRA-intensity-patterns; ii) evaluate the repeatability of HRA-intensity-patterns for the three cardinal planes and the resultant accelerations of the COM during single-leg balance using multiple measures of repeatability (intraclass correlation coefficient, standard error of the measurement, and the reliability coefficient).
Method
Participants
Five males and five females (mean age=25 ± 3 yr; height=169.4 ± 11.7cm; weight=79.0 ± 16.9kg) were recruited, and consented participation through completion of the Western Oregon University IRB-approved informed consent in accordance with the Declaration of Helsinki. All subjects indicated by self-reported medical history no known physiological or functional conditions that would prohibit them from performing exhaustive exercise for a brief period of time, and no known, recent, or previous injuries that would prevent them from participating. All subjects were recreationally active and able to perform the required single-legged protocol.
Participants reported having at least 2-hours rest from exercise and 12-hour abstention from alcohol, caffeine, and any medication that affects the central nervous system. Testing days were separated by no more than seven days. The single-legged protocol has been detailed previously [9,22] and has been demonstrated reliable [9].
Single-legged stances
A series of five dominant-leg stances were performed on three occasions while standing on the dominant leg (determined by preferred kicking leg) for 15-seconds with the participant crossing the arms over the chest and flexing the non-dominant knee to 90 degrees (visually confirmed). Each stance was separated by a 30-s rest period. The duration of the stances was selected as to minimize possible fatigue and to ensure that the participants would be able to maintain balance for the duration of the stance.
COM acceleration
A wireless accelerometer (G-Link®, ± 10g, MicroStrain, Inc., Williston, VT) was fixed with two-sided tape at the intersection of the sagittal and axial planes on the posterior trunk in line with the top of the iliac crest (superficial to L3/L4) at the approximate center of mass (2) and secured with elastic tape (PowerFlex, Andover, MA). The G-Link® integrates two orthogonally mounted dual-axis MEMS accelerometers (ADXL210, Analog Devices, Norwood, MA) and was calibrated according to manufacturer specifications. This accelerometer has been used in previous applications with no limitations [6,9-12].
Triaxial signals from the HRA were streamed in real time to a base station at a frequency of 625Hz and stored on a personal computer for further analysis. COM accelerations were recorded in units of gravity (1g 9.81m s-2) for vertical (VT), medial/lateral (ML), anterior/posterior (AP), and resultant (Res; ) directions.
Intensity analysis
The intensity analysis was performed using R, an open source tool that is easily downloadable from the Internet (www.r-project.org). These steps were described in a previous paper [18] and are based on the methods detailed in von Tscharner [15]. One new to R can find a detailed description [23-25] and demonstration of its application in electromyography and other biosignals in Borg [26,27].
The von Tscharner [15] intensity analysis is based on a set of Cauchy wavelets and defined by the following function:
eqn. 1:
where, ƒ represents the frequency, cf the center frequency, and scale is the scaling function. Center frequency for each wavelet is calculated as:
eqn. 2:
where, cfj is the center frequency of wavelet j (indexed by j=0, 1, 2,…, J - 1), and q and r optimize the spacing of the center frequencies such that the sum of the wavelets is as close as possible to being constant across the desired frequency band. The parameters for J, r, and q are the same for HRA as they are for EMG and MMG. These are J=11 [NOTE: in R, J is indexed 1-11], r=1.959, and q=1.45.
The scaling factor for HRA is somewhat arbitrary in the present methods. Armstrong et al. [18] have determined that, for balance and gait, scale might optimally be set between scale=4.0 and scale=5.6. For present HRA data, scale=5.6 was selected because it provides a center frequency range of 0.37 to 21.18Hz, suitable for single-legged posture. Additionally, no Gaussian filter was applied, as the researchers considered that the filter would do little to correct the "pure" intensity signal and thus offers one greater flexibility in adjusting the scaling factor to suite one's application [18]. The resulting center frequencies are shown in table 1.
![]()
Table 1: Wavelet center frequencies
View Table 1
Details of the output of the intensity analysis are provided elsewhere [15-18]. In brief: Total intensity (In) refers to the sum of the intensities over the wavelet domains 1-J for each sample in time and is calculated as:
eqn. 3:
where, typically, J = 11.
The intensity spectrum (Ij) refers to the sum of the intensities for each center frequency over time and is calculated as:
eqn. 4:
j is the wavelet domain and N is the total number of samples.
Defining p-space
The R code presented in Armstrong et al. [18] details the functions necessary to carry out the computations for the intensity analysis for HRA. The steps for defining p-space are based upon the matrices defined in von Tscharner [19,20] and Castells et al. [21].
The first step in determining p-space is to stack the intensity data for each axis of each trial to create an N·J·k (sample by number of wavelets by number of trials) matrix for each axis. Thus, each measured intensity pattern is represented as a long pattern vector, called a "data-vector" with (N·J) rows. All of the data-vectors for the measured trials form the matrix DATA [19,20].
From the DATA matrix, the correlation matrix and subsequent eigenvalues and eigenvectors are obtained [19,20]:
eqn. 5:
In R, this is accomplished by the function: patternEstar2 <- function(DATA, ke=min(12, ncol(DATA)), normalizeD=FALSE, normalizeE=FALSE) (see Appendix), where DATA is the matrix of data in k columns, and each column represents one trial; ke is the number of eigenvalues to be recorded; and normalizeD and normalizeE allow for the normalization of the values in the DATA columns and output eigenvectors of E, respectively, to unit vectors by indicating "TRUE". The function, patternEstar2, returns the following list: "vectors"=E, "vectorsEE" = EE, and "values"=Es$values.
S <- t(DATA) %*% DATA/K corresponds to eqn. 5, thus providing the correlation matrix. The eigenvalues and eigenvectors are found by: Es <- eigen(S, symmetric=TRUE). The output Es is a list objects with the eigenvectors in Es$vectors and the corresponding eigenvalues, ordered from largest to smallest, in Es$values. Thus, in the projection of the data on the first (i.e., largest) eigenvectors one determines the principle components (p-vectors). The eigenvectors are converted to the eigenvalues of the original correlation matrix by EE <- Es$vectors[,1:ke] and E <- DATA %*% EE.
P-space is calculated by the function: pspaceD <- function (d, E, inverse=FALSE, kmax=ncol(Es$vectors). If inverse=TRUE one takes p-vector and returns space representation; otherwise, if inverse=FALSE, p-vector is returned. In the present study, p-space is called by: X <- pspaceD (d=DATA[,k], E=E), where k is the trial for which p-space is being determined. For each axis and for the resultant accelerations, X was determined for each trial for each subjects and organized for statistical analysis.
Statistical analysis
The data were analyzed to test reliability, i.e., repeatability, via i) the effect of repeated trials and ii) the effects of repeated sessions. Because trials were repeated five times for each session, it was of interest whether there was a learning effect that might be identified among the data in p-space. It was also of interest whether the repeated trials produced a learning effect. Thus, the HRA data from the 15 trials and 3 sessions were analyzed as follows:
To test for the repeatabilty of the data, repeated measures ANOVA were performed on the the k (i.e., 3) principle patterns (i.e., p-vectors) of the 15 trials on the principle patterns of the average HRA-intensity-pattern (of the 5 trials) for each session. From the ANOVA results intraclass correlation coefficients (ICC(A,1)), standard error of the measurement (SEM), and the reliability coefficient (CR) were calculated. SEM and CE were calculated according to the following equations [28-30].
eqn. 6:
eqn. 7:
All statistical analyses were performed using R and significance was set at an alpha level of 0.05.
Results
The median, 25th and 75th quartiles for the 3 principle patterns or p-vectors (P-1, P-2, P-3) for each axis, session, and trial are reported in table 2. The first principle pattern (P-1) describes the greatest amount of variability among the intensity analyses. In all analyses, there was a significant difference between the p-vectors with the P-1 demonstrating median values between ± 0.48 to ± 0.92.
![]()
Table 2: Median (25th to 75th percentiles) scores for each p-vector for the x (vertical), y (medial-later), z (anterior- posterior), and resultant (
) directions
View Table 2
For the repeated measures ANOVA of the p-vectors, the only significant differences were observed for the within Session effects for P-1 and P-2 in the AP direction (p=0.042 and 0.022, respectively), within Trials for P-2 in the AP direction (p=0.042), and within Sessions for P-1 for the Res direction (p=0.027).
ICC(A,1), SEM, and CR for the p-vectors for each axis are presented in tables 3 and 4. Intraclass correlation coefficients were low (±0.07) for all p-vectors except for P-1 for the medial-lateral direction (ICC(A,1)=0.961 (95% CI between 0.918 and 0.988; p<0.001).
![]()
Table 3: Comparison measures of reliability for p-vectors for each acceleration direction (X=Vertical; Y=Medial-lateral; Z=Anterior-posterior; and Res =
), including intraclass correlation coefficient (ICC(A,1)), standard error of the measurement (
), and the reliability coefficient (
). [*p ≤ 0.05]
View Table 3
![]()
Table 4: Comparison measures of reliability for p-vectors averaged across sessions for each acceleration direction (X=Vertical; Y=Medial-lateral; Z=Anterior-posterior; and Res =
), including intraclass correlation coefficient (ICC), standard error of the measurement (
), and the reliability coefficient (
)
View Table 4
Discussion
Signals such as sEMG, MMG, and HRA are nonstationary, i.e., the frequency of the signal varies over time. Thus, averaging a measurable component of such a signal over time may result in a loss of information. To account for the nonstationarity of the signal, the intensity analysis is useful [15-18,22].
Using the HRA-intensity-pattern is a novel approach to examining changes in postural balance. Armstrong et al. [18] describe a method of applying the von Tscharner [15] intensity analysis to HRA. The reliability of data obtained under a variety of HRA applications has been untested. The present study sought to determine the repeatability of HRA-intensity-patterns obtained during repeated single-legged stances.
The investigators examined HRA-intensity-patterns using statistical pattern recognition techniques similar to those described by von Tscharner [19,20] for sEMG and Castells et al. [21] for ECG. The data included single-legged stances repeated across 3 sessions, each including 5 trials. HRA data included acceleration in the VT, ML, and AP directions, as well as the calculated resultant acceleration (Res; ). To examine any possible learning effects and to establish best practice, the data were compared using the individual trials, as well as the average of the 5 trials for each session. In all comparisons, the first principle pattern accounted for the greatest vector distances among the signals (approximately 0.60-0.84 for individual trials). There were notable variations in the acceleration patterns among the trials and sessions, particularly in the anterior-posterior direction. These likely reflect the variability in the motor control strategies. Overall, the analyses reveal little consistency among the p-vectors in repeated measurements.
Because there is considerable variability among the postural control strategies, it is not recommended that the p-vectors for the HRA-intensity-analysis be considered as a stand-alone measurement of postural control. Using the same accelerations presented here, Armstrong et al. [9] and McGregor et al. [6] demonstrated consistency in the peak-to-peak amplitudes and control entropy (a measure of the constraints on the system), respectively. Therefore, each axis, as well as the resultant acceleration should be considered in light of other measures, e.g., peak-to-peak acceleration and multi-site EMG/MMG and/or other kinematic data.
Given the complexity of the intensity output, researchers are challenged to find methods of assessing changes in the intensity-pattern that are not so mathematically complicated that they are not attainable to most clinicians. The present analyses suggest that the examination of individual p-vectors for the HRA-intensity-pattern has little value in assessing changes in postural control. In evaluating the complex, three-dimensional HRA-intensity pattern (i.e., time, frequency, intensity), researchers are limited by the two-dimensional nature of traditional statistical measures of repeatability. ICC, SEM, and CR are based off of repeated measures ANOVA. The methods applied in the present study result in a series of three p-vectors for movement in three directional planes. These values are, however, interrelated and are not adequately evaluated individually
Conclusion
The current paper has presented only one approach to assessing the repeatability of the HRA-intensity-pattern. In all, the researcher must consider what signal information is important and analyze the data accordingly. With the intent of examining the complex HRA-intensity-pattern across multiple trials, the p-space analysis suggested by von Tscharner [19] and von Tscharner and Goepfert [20] may still be a useful, albeit unreliable by current methods, tool in the assessment of balance. Further examination of methods for quantifying HRA in p-space is warranted. Von Tscharner and others [14], for example, have explored using the combination of principle component analysis, individual component analysis, and support vector machines in analyzing human gait patterns.
References
-
Blaszczyk JW, Lowe DL, Hanson PD (1994) Ranges of postural stability and their changes in the elderly. Gait Posture 2: 11-17.
-
Ushiyama J, Masani K (2011) Relation between postural stability and plantar flexors muscle volume in young males. Med Sci Sports Exerc 43: 2089-2094.
-
Moe-Nilssen R (1998) Test-retest reliability of trunk accelerometry during standing and walking. Arch Phys Med Rehabil 79: 1377-1385.
-
Moe-Nilssen R, Helbostad JL (2002) Trunk accelerometry as a measure of balance control during quiet standing. Gait Posture 16: 60-68.
-
Heebner NR, Akins JS, Lephart SM, Sell TC (2015) Reliability and validity of an accelerometry based measure of static and dynamic postural stability in healthy and active individuals. Gait Posture 41: 535-539.
-
McGregor SJ, Busa MA, Yaggie JA, Bollt EM (2009) High resolution MEMS accelerometers to estimate VO2 and compare running mechanics between highly trained inter-collegiate and untrained runners. PLoS One 4: e7355.
-
Rispens SM, Pijnappels M, van Schooten KS, Beek PJ, Daffertshofer A, et al. (2014) Consistency of gait characteristics as determined from acceleration data collected at different trunk locations. Gait Posture 40: 187-192.
-
van Schooten KS, Rispens SM, Pijnappels M, Daffertshofer A, van Dieen JH (2013) Assessing gait stability: the influence of state space reconstruction on inter- and intra-day reliability of local dynamic stability during over-ground walking. J Biomech 46: 137-141.
-
Armstrong WJ, McGregor SJ, Yaggie JA, Bailey JJ, Johnson SM, et al. (2010) Reliability of mechanomyography and triaxial accelerometry in the assessment of balance. J Electromyogr Kinesiol 20: 726-731.
-
McGregor SJ, Armstrong WJ, Yaggie JA, Bollt EM, Parshad R, et al. (2011) Lower extremity fatigue increases complexity of postural control during a single-legged stance. J Neuroeng Rehabil 8: 43.
-
McGregor SJ, Busa MA, Parshad R, Yaggie JA, Bollt EM (2011) Control Entropy of Gait: Does Running Fitness Affect Complexity Of Walking? Clin Kinesiol 65: 9-17.
-
Parshad RD, McGregor SJ, Busa MA, Skufca JD, Bollt E (2012) A statistical approach to the use of control entropy identifies differences in constraints of gait in highly trained versus untrained runners. Math Biosci Eng 9: 123-145.
-
Daffertshofer A, Lamoth CJ, Meijer OG, Beek PJ (2004) PCA in studying coordination and variability: a tutorial. Clin Biomech (Bristol, Avon) 19: 415-428.
-
von Tscharner V, Enders H, Maurer C (2013) Subspace identification and classification of healthy human gait. PLoS One 8: e65063.
-
von Tscharner V (2000) Intensity analysis in time-frequency space of surface myoelectric signals by wavelets of specified resolution. J Electromyogr Kinesiol 10: 433-445.
-
Beck TW, von Tscharner V, Housh TJ, Cramer JT, Weir JP, et al. (2008) Time/frequency events of surface mechanomyographic signals resolved by nonlinearly scaled wavelets. Biomed Sig Process Control 3: 255-266
-
Armstrong WJ, Beck TW, Welch JD, Borg F (2011) Technical Note: Clinical Application of the Intensity Analysis Using the R Open Source Software. Clin Kinesiol 65: 57-67.
-
Armstrong WJ, McGregor SJ, Yaggie, Borg F, Beck TW (2014) Technical Note: Application of the "Intensity Analysis" to High-Resolution Accelerometry. Clin Kinesiol 68: 1-8.
-
von Tscharner V (2002) Time-frequency and principal-component methods for the analysis of EMGs recorded during a mildly fatiguing exercise on a cycle ergometer. J Electromyogr Kinesiol 12: 479-492.
-
von Tscharner V, Goepfert B (2003) Gender dependent EMGs of runners resolved by time/frequency and principal pattern analysis. J Electromyogr Kinesiol 13: 253-272.
-
Castells F, Laguna P, Sörnmo L, Bollmann A, Millet Roig J (2006) Principal Component Analysis in ECG Signal Processing. EURASIP J Adv Signal Process.
-
Armstrong WJ (2011) Wavelet-based intensity analysis of mechanomyographic signals during single-legged stance following fatigue. J Electromyogr Kinesiol 21: 803-810.
-
Smith SW (1997) The Scientist and Engineer's Guide to Digital Signal Processing. San Diego: California Technical Publishing, USA.
-
Teetor (2011) PR Cookbook. Sepastopol, CA: O'Reilly Media.
-
Venerables WN, Smith DM (2010) An Introduction to R (Version 2.11.1).
-
Borg F (2003) Filter banks and the "intensity analysis" of EMG.
-
Borg F (2014) Analyzing biosignals using the R freeware (open source) tool.
-
Vaz S, Falkmer T, Passmore AE, Parsons R, Andreou P (2013) The case for using the repeatability coefficient when calculating test-retest reliability. PLoS One 8: e73990.
-
Weir JP (2005) Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J Strength Cond Res 19: 231-240.
-
Wolak ME, Fairbairn DJ, Paulsen YR (2012) Guidelines for estimating repeatability. Methods Ecol Evol 3: 129-137.